Homework

1
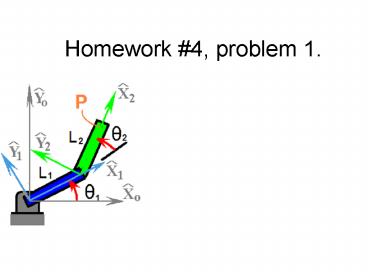
Homework 4, problem 1.
2
Homework 4, problem 1.
3
Frames 0 and 1 share a common origin.
4
Frames 0 and 1 share a common origin.
5
Z axes are permanently aligned in 0 and 1 frames.
6
Angle between the two X axes is q1.
7
Angle between the two X axes is q1.
8
Note angle between X direction of 0 frame and Y
direction of 1 frame is p/2q1
9
Simplifying trig identity.
10
Simplifying trig identity.
11
(No Transcript)
12
Consider next the homogeneous transformation
matrix between the 1 and 2 frames.
13
The direction cosine matrix is the same as
before, replacing q1 with q2
14
The two origins this time are separated by L1
along the X1 direction.
15
The two origins this time are separated by L1
along the X1 direction.
16
Note that regardless of how the robot may move
point P is permanently a distance L2 along the X2
direction.
17
Note that regardless of how the robot may move
point P is permanently a distance L2 along the X2
direction.
18
Note that regardless of how the robot may move
point P is permanently a distance L2 along the X2
direction.
19
(No Transcript)
20
(No Transcript)
21
(No Transcript)
22
(No Transcript)
23
(No Transcript)
24
Problem 3.
25
Find the 2-4 element of the inverse of this
matrix.
26
The 2-4 element relates to the relative position
of the AB origins.
27
Reverse sign.
28
Find the 2-4 element of the inverse of this
matrix.
29
Find the 2-4 element of the inverse of this
matrix.
30
Note that if you applyMatlab, for example
31
Note that if you applyMatlab, for example
32
Which is right?
33
Original T matrix not quite a true homog. trans.
matrix.
34
For example, rows of rotation matrix dont sum
sq. to 1.0.
35
Hence the inverse isnt exactly a h.t. matrix
either.
36
From last time Homogeneous transformation matrix
for the blue link.
37
Since the two frames share their origin, a1d20
38
Since the two frames share their origin, a1d20
39
Recall the one-one element of the h.t. matrix
for link i-1 using the Denavit- Hartenberg convn.
40
(No Transcript)
41
(No Transcript)
42
(No Transcript)
43
Now the one-two element of the h.t. matrix
for link i-1 using the Denavit- Hartenberg convn.
44
(No Transcript)
45
(No Transcript)
46
(No Transcript)
47
(No Transcript)
48
(No Transcript)
49
The component of Yi that lies in the plane of
Zi-1 Yi-1 is the component that is
perpendicular to Xi-1.
50
The component of Yi that lies in the plane of
Zi-1 Yi-1 is the component that is
perpendicular to Xi-1.
51
The component of Yi that lies in the plane of
Zi-1 Yi-1 is the component that is
perpendicular to Xi-1.
52
The component of Yi that lies in the plane of
Zi-1 Yi-1 is the component that is
perpendicular to Xi-1.
53
(No Transcript)
54
(No Transcript)
55
(No Transcript)
56
But what about a1?
57
But what about a1?
58
But what about a1?
59
Homogeneous transformation matrix for blue link.
60
Consider next the yellow link.
61
For the yellow member, link i-1 is link 2.
62
Note that the q2 and q3 axes are parallel.
63
Distance between parallel axes is a2.
64
To determine d3 we locate the origin of the
reference frame that moves with the orange member
...
65
... that being the 3-frame.
66
The origin of the 3 frame must lie along the axis
of rotation of q3.
67
The origin of the 3 frame must lie along the axis
of rotation of q3.
68
The origin of the 3 frame must lie along the axis
of rotation of q3.
69
(No Transcript)
70
(No Transcript)
71
(No Transcript)
72
(No Transcript)
73
(No Transcript)
74
Consider a magnification of the orange link.
75
(No Transcript)
76
Wrist center
77
Axis of rotation of q4.
78
Axis of rotation of q4.
79
(No Transcript)
80
(No Transcript)
81
(No Transcript)
82
(No Transcript)
83
a3
84
d3
85
(No Transcript)
86
What about a2 ?
87
What about a2 ?
88
Consecutive Z axes are parallel therefore, a2 0
89
Note that in the position shown, q30.
90
Note that in the position shown, q30.
91
Note that in the position shown, q30.
92
Note that in the position shown, q30.
93
Homogeneous transformation matrix for the yellow
link for a20.