Writing Skills

1
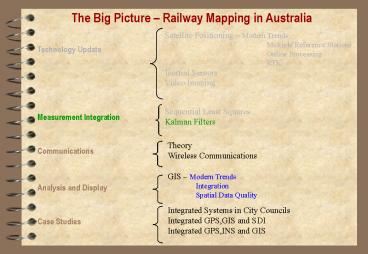
The Big Picture Railway Mapping in Australia
Satellite Positioning Modern Trends

Multiple Reference Stations
Online
Processing
RTK Inertial Sensors Video
Imaging
Technology Update
Sequential Least Squares Kalman Filters
Measurement Integration
Theory Wireless Communications
Communications
GIS Modern Trends Integration
Spatial Data Quality
Analysis and Display
Integrated Systems in City Councils Integrated
GPS,GIS and SDI Integrated GPS,INS and GIS
Case Studies
2
451-446 Integrated Systems in Geomatics

• Lecture 7 Kalman Filtering

3
Used for problems in which the parameters being
estimated by the least squares process vary with
time, eg navigation
ti
t3
t2
ti is the present, tj is the time we want to
estimate the position ti tj we are
filtering ti gt tj we are smoothing ti lt tj we are
predicting
t1
4
Example

• A ship at sea carrying out a seismic survey. It
  would be common to travel in straight lines,
  taking seismic measurements at specified linear
  intervals, whilst continuously interrogating some
  kind of shore based navigation system. The
  process of computing the ship's position at any
  instant in order to plot the real-time position
  on a chart would be filtering. The computation
  of the time at which the ship is expected to make
  a seismic measurement would be predicting and the
  subsequent, possible office based estimation of
  where the ship actually was when the measurements
  were taken would be smoothing.

5
i. Prediction This provides an estimate of the
'state' of the vehicle at some future point in
time using the vehicle's present results
(positions, velocities etc. and their associated
precisions) as well as the model of the vehicle's
movement. ii. Filtering This provides an
estimate of the system 'state' at the current
point in time by incorporating the predicted
results with all of the position data now
available. iii. Smoothing This gives an
estimate of previous system 'state' when all the
filtered and predicted results from previous
epochs are post processed. By doing this better
results can be obtained for these epochs.
6
Applications of Kalman Filtering
Navigation Kalman filters have been used
extensively for navigation in the marine and
space environments, and have been developed to
incorporate most positioning systems. It has
only limited use within the realms of land
vehicle navigation, and models for this
application will be discussed later in this
thesis. Range Processing The range from a gps
satellite can be predicted, as long as the
movement of both the satellite and the receiver
can be modelled. In this case the Kalman filter
can be applied to the residuals of the range
measurements, and the filtered ranges used to
compute the position of the receiver through a
resection.
7
Applications of Kalman Filtering
Pseudorange smoothing Both the gps pseudorange
and phase observables can be predicted for future
epochs. The actual pseudorange values can then
be combined with the phase observations within
the filtered solution to create the so-called
"phase-smoothed pseudoranges". Orbit
computations Kalman filters can be applied to
predicting the Keplarian elements contained
within the gps navigation message. Using the
tracking data from monitor stations a filtered
solution is obtained at the gps Control Segment.
More predictions based on these values are then
made, which are subsequently uploaded to the
satellites.
8
Applications of Kalman Filtering
Integer ambiguity resolution The Kalman filter
may be used to help resolve the integer number of
cycles ambiguity for phase processing. Performance
monitoring The Kalman filter is an ideal tool
for the integrity monitoring of the gps system.
9
To derive solutions for each of the estimation
problems outlined previously, the Kalman filter
makes use of information from two sources i. The
'raw' uncorrelated observations. ii Some
knowledge of how the vehicle has moved in the
past and therefore how it may be expected to move
in the future. This model of behaviour is
updated with each new element of observational
data.
10
i. The measurement, functional or primary model,
which relates the unknown parameters to the
observations. ii. The dynamic, kinematic, or
secondary model, which relates the unknown
parameters at epoch to those at epoch .
11
State Vector
The state vector is a vector of parameters which
are to be estimated within the Kalman filtering
algorithms. It not only contains the desired
parameters, but other values necessary to model
the dynamic behaviour of the vehicle. If the
system under consideration is that of a moving
vehicle, with a positioning system providing
regular updates of the easting and northing
position, then the state vector may consist of
12
The Measurement Model
The measurement model relates the parameters in
the state vector to the observed quantities.
13
Dynamic Model
This model is based on knowledge of how the state
vector is expected to vary with time. In its most
general form, the functional relationship of the
dynamic model may be represented as
14
Summary of Kalman Filter Equations

• Obtain least squares estimate x1 and its
  covariance matrix Cx using the measurements l1

15
Example - Kalman filtering
D
C
i
True Path
5
6
E
3
A
4
2
B
1
16
Example - Kalman filtering
This example follows the navigation problem
outlined. Like least squares the Kalman filter
is recursive and takes some time to settle
down. This example enters the process after the
i-1th recursion and simply illustrates the
numerical process of carrying out one complete
set of calculations for filtering, prediction and
smoothing.
17
(No Transcript)
18
Class Exercise
Verify that if at point i 1 we have the
observations of
then the filtered, predicted and smoothed results
at points i 1, i 2 and i respectively would be