Root Locus and Lead Controllers - PowerPoint PPT Presentation
1 / 19
Title:
Root Locus and Lead Controllers
Description:
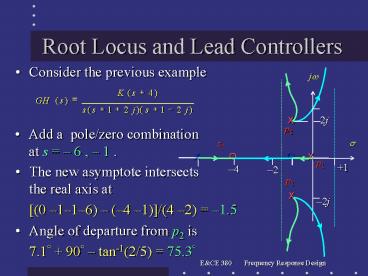
... p2 is. 7.1 90 tan-1(2/5) = 75.3 The new asymptote intersects ... shifts the asymptote real axis intersection to the left. modifies the angle criterion by ... – PowerPoint PPT presentation
Number of Views:74
Avg rating:3.0/5.0
Title: Root Locus and Lead Controllers
1
Root Locus and Lead Controllers
- Consider the previous example
- Add a pole/zero combinationat s 6 , 1 .
X
O
- The new asymptote intersectsthe real axis at
- (0 116) (4 1)/(4 2) 1.5
- Angle of departure from p2 is
- 7.1 90 tan-1(2/5) 75.3
2
Root Locus Lead Design
- Consider again the system defined by
Design Point
- Control design specifications
? ? 0.707
settling time ? 1.0 s
? ? ? ? 4
3
Root Locus Lead Design
- Can we force the root locus to go through the
design point, s1 ?
- Consider the effect of adding a pole and zero
combination (a lead compenstor).
X
4
Root Locus Lead Design
- Three effects of the pole zero combination
- modifies the real axis segments
- shifts the asymptote real axis intersection to
the left - modifies the angle criterion by
- ? ? ?z ? ?p
5
Root Locus Lead Design
- Design steps
- place the zero below the design point, s1
(approx.)
- determine the angle difference, ? ? 90 ? ?p that
will satisfy the angle criterion for the design
point, s1 .
- locate the pole location from the angle, ?p and
the location of the zero
6
Root Locus Lead Design
- calculate ?p
? ?135 ? 116.6 ? 180 ? ? 431.6 or 71.6 ? ?p
? 90 ? 71.6 ? 18.4
18.4
X
16
- calculate the pole location
tan(18.4) ? 4 / (? 4 ? p) ? p ? ?4/0.333 ? 4
? ? 16
7
Root Locus Lead Design
- The asymptote intersection
? ?a ? ? 7
- Determine the gain at the design point
K ? 5.56 4.47 12.65 / 4 ? 78.6
8
Root Locus Lead Design
- The final compensator is
- The final closed-loop systems is
Note the lead compensator ? ? 16/4 ? 4
- The compensated open-loops system is
9
(No Transcript)
10
Root Locus Lag Design
- Pole/zero placement
- The lag compensator is represented by a pole near
the imaginary axis and a zero further to the left.
- Low frequency gain
- The compensator low frequency gain is
11
Root Locus Lag Design
- Desired effects of the lag
- increase the low frequency gain to achieve
desired steady-state error specifications, the
gain increase is ?? .
- Introduce very little effect on the path of the
root locus, ie.
12
Root Locus Lag Design
- Relate the angle requirement and low frequency
gain (note 2 0.035 rad.) By similar triangles
L
then
?
13
Root Locus Lag Design
- Design steps
- Determine a point, s1 on the uncompensated loci
that satisfies the dynamic requirements. - Find the gain at s1 and then the low frequency
gain of the system. - Determine the low frequency gain, ?? of the
compensator required to meet the system
steady-state error requirement.
- Calculate the compensator pole location using s1
and ?? in the relationship
- Finally, calculate the compensator zero from
14
Root Locus Lag Design Example
- Consider again the system defined by
K 2 2 /1 4
- Control design specifications
? ? 0.50
ess ? 5 for a ramp input.
15
Root Locus Lag Design Example
- The velocity steady-state error constant is
- The compensator pole magnitude is
For ess ? 0.05, Kv ? 20
0.0128
- The compensator zero magnitude is
- Therefore the compensator low-frequency gain must
be ?? ? 10 .
z ?? p 0.128
16
Root Locus Lag Design Example
- The final compensator is
- The final closed-loop systems is
- The compensated open-loops system is
- The roots of the final closed-loop systems are
s -0.9386 1.7000i s -0.1358
17
Root Locus of Final System
x
18
Step Responses
uncompensated
19
Ramp Response