Ch 7 The Crystalline Solid State - PowerPoint PPT Presentation
1 / 15
Title:
Ch 7 The Crystalline Solid State
Description:
Zinc Blende Structure: ZnS. Same as diamond structure with alternating Zn and S atoms ... Rarer than Zinc Blende structure for ZnS; formed at higher Temperatures ... – PowerPoint PPT presentation
Number of Views:73
Avg rating:3.0/5.0
Title: Ch 7 The Crystalline Solid State
1
Ch 7 The Crystalline Solid State
- Formulas and Structures
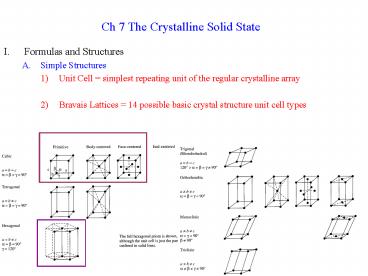
- Simple Structures
- Unit Cell simplest repeating unit of the
regular crystalline array - Bravais Lattices 14 possible basic crystal
structure unit cell types
2
- Atoms on corners and edges are shared between
unit cells - Rectangular corners shared by 8 unit cells (8 x
1/8 1 total atom in cell) - Other corners shared unequally, but still
contribute 1 atom to unit cell - Edges shared by 4 cells, contribute (4 x ¼ 1
atom to unit cell) - Faces shared by 2 cells, contribute ½ atom to
each - Angles and Dimensions can vary triclinic has all
different lengths and angles - Lattice Points positions of atoms needed to
generate the whole crystal - Body Centered Cubic (0,0,0) origin and (½ ,
½, ½) center - All other atoms can be generated from these 2 by
moving them exactly one cell length - Cubic Structures
- Primitive Cubic is the simplest type
- To fully describe length of side, 90o angles,
(0,0,0) lattice point - 8 x 1/8 1 atom in the unit cell
- each atom surrounded by 6 others (Coordination
Number CN 6) - Not efficiently packed only 52.4 of volume is
occupied (74.1 max) - Vacant space at center with CN 8 0.73r
sphere would fit here
3
- Body-Centered Cubic (bcc)
- One more atom is added to the center of the cube
- Size of unit cell must increase over simple cubic
- Diagonal across center 4r (r radius of one
atom) - Corner atoms not in contact with each other due
to cell size expansion - Side 2.31r (Calculate this in Ex. 7-1)
- Unit cell contains 1(1) 8(1/8) 2 atoms
- Lattice Points (0,0,0) and ( ½ , ½ , ½ )
- Close-Packed Structures
- Spheres will arrange to take up the least space,
not cubic or bcc - Two structures have almost identical packing
efficiency (74.1) - Hexagonal Close Packing (hcp)
- Cubic Close Packing (ccp) Face-Centered Cubic
(fcc) - Both have CN 12 for each atom 6 in its layer,
3 above, and 3 below - HCP has 3rd layer in identical position as first
ABA second layer above holes CCP has 3rd layer
displaced so above holes in first layer ABC - Both have 2 tetrahedral (Td) holes per atom (CN
4) formed by 3 atoms in one layer and one atom
above/below - Both have 1 octahedral (Oh) hole per atom (CN
6) formed by 3 atoms in one layer and 3 atoms
above/below
APF 68.0 CN 8
4r
l
l
4
(No Transcript)
5
- HCP unit cell is smaller than the hexagonal prism
- Take four touching atoms in 1st layer and extend
lines up to 3rd layer - 8(1/8) 1 2 atoms in unit cell
- Dimensions 2r, 2r, and 2.83r
- Angles 120o, 90o, and 90o
- Lattice Points (0,0,0,) and ( 1/3, 2/3, 1/2)
6
- CCP unit cell
- One corner from layer 1, opposite corner from
layer 4 - 6 atoms each from layers 2 and 3 in the unit cell
- Unit cell is fcc
- 8(1/8) 6(1/2) 4 atoms in the unit cell
- Lattice Points (0,0,0), ( ½ , 0 , ½), ( ½ , ½,
0), (0 , ½ , ½)
7
- Holes
- 2 Td and 1 Oh hole per atom in both (hcp) and
(ccp) - If ionic compound, small cations can fill these
holes - Td hole 0.225r Oh hole 0.414r
- NaCl has Cl- in (ccp) with Na (ccp) but also in
the Oh holes - Na 0.695r, so it forces the Cl- to be farther
apart, but still CN 6 - Metallic Crystals
- Most metals crystallize in (bcc), (ccp), or (hcp)
structures - Changing pressure or temperature can interchange
these forms for a metal - Must consider bonding, not just geometric packing
only - Soft and malleable metals usually have (ccp)
structure (copper) - Harder and more brittle metals usually have the
(hcp) structure (zinc) - Most metals can be bent due to non-directional
bonding - Weak bonding to all neighbors, not strong bonding
to any single one - Atoms can slide past each other and then realign
into crystal form - Dislocations imperfections in lattice make it
easier to bend - Impurities other elements allow slippage of
layers - Work Hardening hammer until impurities are
together
A summary
8
FCC elements
HCP elements
9
- Diamond
- Each atom is tetrahedrally bonded to 4 other
carbon atoms - Directional single bonds, unlike metals, cause
hardness - Binary Compound Structures
- Simplest structures just have 2nd element in
holes of the first elements lattice - Small cations can fit in Td/Oh holes of large
anions - Large cations may only be able to fit in Oh holes
- Even larger cations may cause changes in
structure if they dont fit in holes - Relative Number of Cations/Anions
- M2X wont allow close-packing of anion lattice
with cations in Oh holes because there are more
cations than holes - Alternatives cations in Td holes, vacancies, not
close-packed
10
- Sodium Chloride Structure NaCl
- Na in (fcc) and Cl- in (fcc)
- Offset by ½ unit cell length
- Na are centered in edges of Cl- lattice (or vice
versa) - Most alkali halides have this same structure
- Large size difference of ions facilitate this
structure - Each Cl- has CN 6 Na Each Na has CN 6
Cl- - Cesium Chloride Structure CsCl
- Cs in simple cubic structure with Cl- in center
(or vice versa) - Cl- 0.83Cs size (0.73r in center is ideal)
- Rare structure, need big cation (Cs, Tl only
cations known with this structure)
11
- Zinc Blende Structure ZnS
- Same as diamond structure with alternating Zn and
S atoms - Alternate Zn and S each in (fcc) lattices
combined so each ion is in a Td hole of the other
lattice - Stoichiometry only ½ of the Td holes are
occupied and ½ are vacant - Wurtzite Structure ZnS
- Rarer than Zinc Blende structure for ZnS formed
at higher Temperatures - Zn and S each in (hcp) lattices combined so each
ion is in a Td hole of the other lattice - Again, ½ of the Td holes are vacant
12
- Fluorite Structure CaF2
- Ca2 in (ccp) lattice with 8 F- surrounding each
and occupying all Td holes - Alternate F- in simple cubic lattice with Ca2
in alternate body centers - Nearly perfect radius fits for this structure
- Antifluorite Structure
- Reverse stoichiometry compounds like Na2O
- Every Td hole in the anion lattice is occupied by
a cation
13
- Nickel Arsenide Structure NiAs
- As atoms in close packed layers exactly above
each other - Ni atoms in all the Oh holes
- Both Ni and As have CN 6
- Alternate Ni atoms occupy all Oh holes of (hcp)
As lattice - Usual for MX compounds where X Sn, As, Bi, S,
Se, Te - Rutile Structure TiO2
- Distorted TiO6 octahedra forming columns by
sharing edges - Ti CN 6 O CN 3
- Adjacent columns connected by sharing corners of
octahedra - Unit cell has Ti at corners and in the body
center, 4 O in the faces, and 2 O in the plane of
the body center Ti - MgF2, ZnF2 are other examples
14
- The Radius Ratio
- We can crudely predict CN by using the ratio
r/r- - This assumes atoms are just packing as hard
spheres (not really all that occurs) - Examples
- NaCl r/r- 113/167 (CN 4) 0.667
- r/r- 116/167 (CN 6) 0.695 Fits best
with CN 6 - ZnS r/r- 74/170 (CN 4) 0.435 Fits best
with CN 4 - r/r- 88/170 (CN 6) 0.518 CN 4 in
actual structure - 4) Exercise 7-2 CaF2 has fluoride ions in a
simple cubic array and calcium ions in alternate
body centers, with r/r- 0.97. What are the
coordination numbers of the two ions predicted by
r/r- ? What are the coordination numbers
observed? Predict coordination numbers of Ca2
in CaCl2 and CaBr2.
Appendix B1
15
A summary of what you learn.
- 7 Crystal systems different lattice centering
- ?14 unique Bravais lattices
- Cubic unit cells
- Simple (primitive),
- bcc
- fcc (ccp)
- Hexagonal unit cells.
- hcp
- Close packing
- Packing efficiency
- CN 6 lt 8 lt12
- Simple cubic lt bcc lt fcc hcp (calculation
required) - Holes
- Cubic hole in simple cubic
- Td hole in fcc and hcp
- Metallic crystals
- Binary ionic compounds
- Anions in close packing structures cations in
holes. - Radius ratio
- Cation/anion ratio
- Typical ionic structures
- NaCl (rock salt structure)
- Cl- in fcc Na in Oh holes
- Na in fcc Cl- in Oh holes
- CsCl
- Cs- in simple cubic Cl- in cubic hole
- Cl- in simple cubic Cs in cubic hole
- Zn Blende
- S- in fcc ½ Zn2 in Td holes
- Wurtzite Structure
- S- in hcp ½ Zn2 in Td holes
- Fluorite structure CaF2