Fixed Parameters: Population Structure, Mutation, Selection, Recombination,...

1
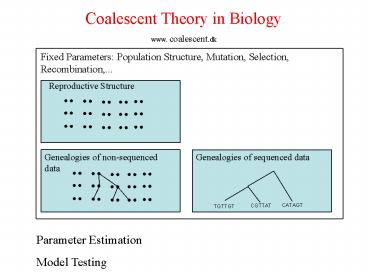
Coalescent Theory in Biology www. coalescent.dk
Fixed Parameters Population Structure, Mutation,
Selection, Recombination,...
Reproductive Structure
Genealogies of non-sequenced data
Genealogies of sequenced data
CATAGT
CGTTAT
TGTTGT
Parameter Estimation Model Testing
2
Wright-Fisher Model of Population Reproduction
Haploid Model
i. Individuals are made by sampling with
replacement in the previous generation. ii. The
probability that 2 alleles have same ancestor in
previous generation is 1/2N

• Assumptions
• Constant population size
• No geography
• No Selection
• No recombination

Diploid Model
Individuals are made by sampling a chromosome
from the female and one from the male previous
generation with replacement
3
P(k)Pk alleles had k distinct parents
1
1
2N
Ancestor choices
k -gt any
k -gt k
k -gt k-1
k -gt j
(2N)k
2N (2N-1) .. (2N-(k-1)) (2N)k
Sk,j - the number of ways to group k labelled
objects into j groups.(Stirling Numbers of second
kind.
For k ltlt 2N
4
Waiting for most recent common ancestor - MRCA
Distribution until 2 alleles had a common
ancestor, X2?
P(X2 gt j) (1-(1/2N))j
P(X2 j) (1-(1/2N))j-1 (1/2N)
P(X2 gt 1) (2N-1)/2N 1-(1/2N)
j
j
2
2
1
1
1
1
1
1
2N
2N
2N
Mean, E(X2) 2N. Ex. 2N 20.000, Generation
time 30 years, E(X2) 600000 years.
5
10 Alleles Ancestry for 15 generations
6
Multiple and Simultaneous Coalescents
1. Simultaneous Events 2. Multifurcations. 3.
Underestimation of Coalescent Rates
7
Discrete ? Continuous Time
1.0 corresponds to 2N generations
1.0
0.0
2
5
6
3
8
The Standard Coalescent
Two independent Processes Continuous
Exponential Waiting Times Discrete
Choosing Pairs to Coalesce.
Waiting
Coalescing
1,2,3,4,5
(1,2)--(3,(4,5))
1,23,4,5
1--2
123,4,5
3--(4,5)
1234,5
4--5
12345
9
Expected Height and Total Branch Length
Branch Lengths
Time Epoch
1
2
1
2
1
1/3
3
2/(k-1)
k
Expected Total height of tree Hk 2(1-1/k)
i.Infinitely many alleles finds 1 allele in
finite time. ii. In takes less than twice as
long for k alleles to find 1 ancestors as it does
for 2 alleles. Expected Total branch length in
tree, Lk 2(1 1/2 1/3 .. 1/(k-1)) ca
2ln(k-1)
10
Effective Populations Size, Ne. In an idealised
Wright-Fisher model i. loss of variation per
generation is 1-1/(2N). ii. Waiting time for
random alleles to find a common ancestor is
2N. Factors that influences Ne i. Variance in
offspring. WF 1. If variance is higher, then
effective population size is smaller. ii.
Population size variation - example k cycle
N1, N2,..,Nk. k/Ne 1/N1.. 1/Nk. N1 10
N2 1000 gt Ne 50.5 iii. Two sexes Ne
4NfNm/(NfNm)I.e. Nf- 10 Nm -1000 Ne - 40
11
6 Realisations with 25 leaves
Observations Variation great close to root.
Trees are unbalanced.
12
Sampling more sequences
The probability that the ancestor of the sample
of size n is in a sub-sample of size k
is Letting n go to infinity gives (k-1)/(k1),
i.e. even for quite small samples it is quite
large.
13
Adding Mutations
m mutation pr. nucleotide pr.generation. L
seq. length µ mL Mutation pr. allele
pr.generation. 2Ne - allele number. Q 4Nµ --
Mutation intensity in scaled process.
Continuous time Continuous sequence
Discrete time Discrete sequence
1/L
time
1/(2Ne)
time
sequence
sequence
mutation
mutation
coalescence
Probability for two genes being
identical P(Coalescence lt Mutation) 1/(1Q).
1
Q/2
Q/2
Note Mutation rate and population size usually
appear together as a product, making separate
estimation difficult.
14
Three Models of Alleles and Mutations.
Finite Site
Infinite Allele
Infinite Site
acgtgctt acgtgcgt acctgcat tcctgcat tcctgcat
Q
Q
Q
acgtgctt acgtgcgt acctgcat tcctggct tcctgcat
i. Allele is represented by a sequence. ii. A
mutation changes nucleotide at chosen position.
i. Only identity, non-identity is
determinable ii. A mutation creates a new type.
i. Allele is represented by a line. ii. A
mutation always hits a new position.
15
Infinite Allele Model
4
5
1
2
3
16
Infinite Site Model
Final Aligned Data Set
17
Labelling and unlabellingpositions and sequences
1
2
3
4
5
Ignoring mutation position
Ignoring sequence label
1
2
3
5
4
Ignoring mutation position Ignoring sequence label


,
,
The forward-backward argument
4 classes of mutation events incompatible with
data
9 coalescence events incompatible with data
18
Infinite Site Model An example
Theta2.12
2
3
2
3
4
5
5
9
5
10
14
19
33
19
Impossible Ancestral States
20
Finite Site Model
acgtgctt acgtgcgt acctgcat tcctgcat tcctgcat s s
s
Final Aligned Data Set
21
Diploid Model with Recombination

• An individual is made by
• The paternal chromosome is taken by picking
  random father.
• Making that fathers chromosomes recombine to
  create the individuals paternal chromosome.
• Similarly for maternal chromosome.

22
The Diploid Model Back in Time.
A recombinant sequence will have have two
different ancestor sequences in the grandparent.
23
1- recombination histories I Branch length change
4
1
2
3
4
1
2
3
24
1- recombination histories II Topology change
4
1
2
3
4
1
2
3
25
1- recombination histories III Same tree
4
1
2
3
4
1
2
3
26
1- recombination histories IV Coalescent time
must be further back in time than recombination
time.
c
r
4
1
2
3
27
Recombination-Coalescence Illustration
Copied from Hudson 1991
Intensities Coales. Recomb.
0 ?
1 (1b)?
b
3 (2b)?
6 2?
3 2?
1 2?
28
Age to oldest most recent common ancestor
29
Number of genetic ancestors to the Human Genome
Sr number of Segments E(Sr) 1 r
time
C
C
C
R
R
R
sequence
Simulations
Statements about number of ancestors are much
harder to make.
30
Applications to Human Genome (Wiuf and Hein,97)
Parameters used 4Ne 20.000 Chromos. 1 263 Mb.
263 cM Chromosome 1 Segments 52.000
Ancestors 6.800 All chromosomes Ancestors
86.000 Physical Population. 1.3-5.0 Mill.
A randomly picked ancestor (ancestral material
comes in batteries!)
31
Ignoring recombination in phylogenetic analysis
General Practice in Analysis of Viral Evolution!!!
Recombination
Assuming No Recombination
Mimics decelerations/accelerations of
evolutionary rates. No Infinite
recombination implies molecular clock.
32
Simulated Example
33
Genotype and Phenotype Covariation Gene Mapping
Sampling Genotypes and Phenotypes
ResultThe Mapping Function
A set of characters. Binary decision
(0,1). Quantitative Character.