Stellar Structure

1
Stellar Structure
0
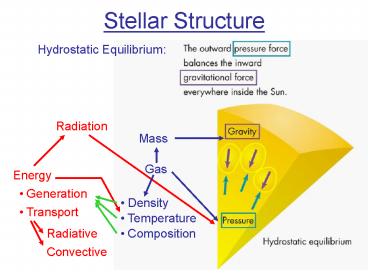
Hydrostatic Equilibrium
Radiation
Mass
Gas
Energy

• Generation

• Density

• Transport

• Temperature

Radiative

• Composition

Convective
2
Hydrostatic Equilibrium
0
A
Fp
Dm
Dr
DFg
Fp
3
The Pressure Integral
0
A
m cosq
q
DA
p
v
Dx
4
Overcoming the Coulomb Barrier
0
? kTcl 1010 K
Ucl (3/2) kTcl
Ut (3/2) kTt
? kTcl 107 K
rt ldeBrogle h/p
5
0
6
0
7
0
8
The PP Chain
0
9
The CNO Cycle
0
p
g
42He
126C
ne
137N
p
157N
e
136C
p
ne
158O
g
e
147N
g
p
10
Binding energy per nucleon
0
Endothermic
Energy can be liberated via nuclear fission
Exothermic
Energy can be liberated via nuclear fusion
11
Convection
0
Adiabatic expansion P Krg
12
Favorable Conditions for Convection
0

• Large Opacities ? Large dT/drrad
• Partial Ionization Zones ? Brings g close to 1 ?
  small dT/drad
• Low g ? small dT/drad g/Cp
• Strongly T-dependent energy generation (CNO
  cycle!) ? large dT/dr

13
Stellar energy transport structure as a function
of stellar mass
0
R/R
1
M/M0
90
0.25
1.3
1.2
0.08
Sun-like stars (0.25 M0 lt M lt 1.2 M0) Radiative
core convective envelope
High-Mass stars (M gt 1.3 M0) Convective core
radiative envelope
Low-mass stars (M lt 0.25 M0) Completely
convective
14
Vogt-Russell Theorem
0

• The mass and composition of a star uniquely
  determine its radius and luminosity, internal
  structure, and subsequent evolution.

gt Almost 1-dimensional Zero-Age Main Sequence
(ZAMS)
15
Masses of Stars in the Hertzsprung-Russell Diagram
0
Masses in units of solar masses
40
18
The higher a stars mass, the more luminous
(brighter) it is
High masses
6
3
L M3.5
1.7
1.0
High-mass stars have much shorter lives than
low-mass stars
Mass
0.8
0.5
tlife M-2.5
Sun 10 billion yr.
Low masses
10 Msun 30 million yr.
0.1 Msun 3 trillion yr.
16
Summary Stellar Structure
0
Convective Core, radiative envelope Energy
generation through CNO Cycle
Sun
Mass
Radiative Core, convective envelope Energy
generation through PP Cycle
17
Energy Transport Structure
0
Inner convective, outer radiative zone
Inner radiative, outer convective zone
CNO cycle dominant
PP chain dominant