A simple slide rule

1
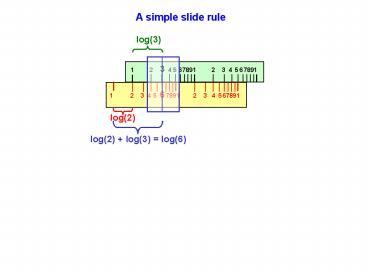
A simple slide rule
log(3)
log(2)
log(2) log(3) log(6)
2
Arithmetic Choices
Fixed-point (FX) Scaled integermanual rescale
after multiply Hard to design, but common
choice for cost-sensitive applications Floating-p
oint IEEE-754 (FP) Exponent provides automatic
scaling for mantissa Easier to use but more
expensive Logarithmic Number System
(LNS) Converts to logarithms oncekeep as log
during computation Easy as FP, can be faster,
cheaper, lower power than FX
3
LNS vs. Conventional
Compared to FP Similar dynamic range but
slightly better precision Cheaper multiply,
divide, square root Compared to FX Same
signal-to-noise ratio with fewer bits Same
dynamic range with fewer bits No scaling
reduce time-to-market High bits change less
frequently power savings Cheaper multiply,
divide, square root
4
Commercial Interest in LNS
Motorola 120MHz LNS 1GFLOP chip
pan99 European Union LNS microprocessor
col00 Yamaha Music Synthesizer
kah98 Boeing Aircraft controls
Interactive Machines,Inc. IMI-500 Animation
for Jay Jay the Jet Plane
5
Notation
Three forms of LNS Unsigned (ULNS)
Signed (SLNS) Redundant
(DRLNS) lower-case variables (e.g., x)
real values, upper-case variables (e.g., X)
corresponding logarithmic representations
b base of the logarithm
(b2 is typical)
6
ULNSUnsigned
Assume all values gt 0 OK for some
applications, like Hidden Markov Modeling
waz95 On input Xlogb(x) During
computation keep as log X is truncated
round-off error slightly better than FP. On
output xbX Advantage Simple as a slide rule
7
SLNSSigned
On input Xlogbx XSsign(x) During
computation Keep track of signs On output
x(-1)XS ? bX Advantage easy to use,
analogous to FP
8
DRLNSRedundant
On input logb(x) x gt 0
- ? x gt 0 XP
XN - ?
x lt 0 logbx x lt
0 During computation Keep track of XP and
XN On output x bXP - bXN Advantage
avoids difficult LNS subtractions
9
Multiplication
ULNS by ULNS Given X logb(x) and Y
logb(y) P X Y.
No additional round-off errors Hardware
1 adder
SLNS by SLNS Given XS sign(x), X
logbx, YS sign(y), Y
logby PS XS ? YS, P X
Y. Hardware 1 adder and 1 XOR
10
Redundant Multiplication
11
Reciprocal, Roots, Powers SLNS and ULNS
Easy operations logb (x2) 2X,
left shift logb (x-1) -X, negation
_ logb (? x ) X/2, right shift
12
AdditionULNS

Given X logb(x) and Y logb(y) Why it
works 1. Let Z X-Y
1. Z logb(x/y) 2. Lookup sb(Z)
logb(1bZ) 2. sb(Z) log b(1x/y) 3.
T Y sb(Z)
3. T logb(y(1x/y))
Thus, T logb(y x) Hardware
1 subtractor, 1 lookup table (ROM or RAM) and 1
adder.
13
AdditionULNS, Direct ROM Table Growth
Bytes Max F Application
This LNS has samehn
32 3.2 100 1 FFT swa83
dynamic range as 15-bit FX 1K 8
100 7 neural net ar n97
convergence as 16-bit FX 2K 6.4 101
5 audio FIR filter sul93 SNR
as 14-bit FX 64K 6.5 104 10 curve
drawing kur91 plots as 16-bit FX 2M
1.7 1038 12 general-purpose DSP tay88
ARRE as 19-bit FX 12G 1.7 1038 23
general-purpose ?P col00 ARRE as
IEEE-754 FP Without reduction, table size
grows exponentially with precision (F).
14
Three ways to reduce table size
Dont tabulate negative Z Sb(-Z) sb(Z)
- Z Dont tabulate for large Z Sb(Z) ? Z if
Z gt F, where F is precision Interpolate
from a smaller table cuts number of address
bits in half
15
Interpolationpartitioned vs. unpartitioned
Methods that partition the range of Z
Distance between tabulated points is non-uniform
Accuracy like IEEE-754 (32-bit word, 23-bit
precision) possible Linear Chebychev hen88
Linear-Taylor lew90 Quadratic-Lagrange
lew94 Quadratic-Taylor-error-correcting
col00 We will instead consider a simpler
Linear Lagrange method Range of Z not
partitioned, accuracy like DSP (20-bit word,
12-bit precision)
16
InterpolationUnpartitioned, Linear-Lagrange
? 2-N uniform spacing between tabulated
points N is of fraction bits in ZH Bus (Z)
split into low part ( 0 lt ZLlt? )
high part ( ZH Z-ZL ) slope
(sb(ZH?)-sb(ZH))/? ? Need
multiplier ? But this multiplier is smaller than
multiplier in FX system!

sb(ZH?)
sb(Z)
sb(ZH)
ZH ZZHZL
ZH?
sb(Z) ? sb(ZH)
((sb(ZH?)-sb(ZH))/?)ZL
ZL
?
slopeZL
17
Interpolation
Accuracy Faithful rounding arn01,ar
n01b Either nearest or next nearest To get F
bits rounded faithfully requires N?(F-4)/2? ROM
needs ?log2(F)? ?(F-4)/2? address
bits Memory savings F (precision) 6 10
12 16 23 Direct bytes 2K 64K 1M 4M 12G Interpo
late bytes 16 128 512 2K 48K
18
InterpolationField Programmable Gate Array (FPGA)
Dual-port memory Two addresses, two outputs,
same table Available in Xilinx Virtex-300
xil99 Increment one address by ? Obtain
sb(ZH?) and sb(ZH) simultaneously Subtract
sb(ZH?) - sb(ZH) to obtain slope
19
ZL
sb(ZH?)


?
sb(Z)
-
Z
dual-port memory

sb(ZH)
ZH
20
SubtractionULNS
Similar to ULNS addition except uses
db(Z)logb1-bZ instead of sb(Z) db harder to
interpolate due to singularity near
Z0 .Partition range of Z with non-uniform ?
lew90,lew94 .Store larger table with smaller ?
in cheap, slow DRAM ar n92 .Defer subtraction
using DRLNS ar n90 .Use co-transformation ar
n98 to convert db to sb db(ZHZL) db(ZL)
sb (ZL db(ZH) db(ZL)), where db(ZH) and
db(ZL) are in tables Use
co-transformation col00 to convert db away
from 0
21
Signed Addition/Subtraction
AdditionSLNS Choose sb or db depending on
whether operand signs are the same
Y sb(X-Y) XS YS XS X gt Y
Y db(X-Y) XS ? YS YS Y gt X
TS
T
SubtractionSLNS Complement YS before SLNS
addition
Addition/SubtractionDRLNS Use sb in parallel to
compute TP and TNdb not required TP
YP sb(XP-YP) TN YN sb(XN-YN)
22
Conclusion
LNS variations Easy
Moderate Hard Functions ULNS
/ ? - sb for
add db for subtract SLNS / ?
- sb and db DRLNS
SLNS - / ? only sb
sb interpolation Interpolation for higher
precision than direct lookup Linear-Lagrange sb
interpolator 20 bit, F12 bits precision Dual
port memory of Xilinx Virtex FPGAs to obtain the
slope
23
References
ar n01b M. Arnold, C. Walter. (June 11-13,
2001). Faithful rounding is good
enough for some LNS applications, 15th
Symposium on Computer Arithmetic, Vail,
CO, IEEE. arn01 M. Arnold. (Apr 19-20, 2001).
A pipelined LNS ALU," IEEE Workshop on
VLSI, Orlando, Florida. arn98 M. G. Arnold,
T. A. Bailey, J. R. Cowles and M. D. Winkel.
(July 1998). Arithmetic co-transformations
in the real and complex logarithmic
number systems," IEEE Trans. Comput., Vol. 47,
No. 7, pp. 777-786. arn97 M. Arnold,
T. A. Bailey, J. J. Cupal and M. D. Winkel.
(June 9-12 1997). On the cost-effectiveness
of logarithmic arithmetic for
back-propagation training on SIND processors,
Intl. Conf. On Neural Networks, Houston,
TX, Vol. 2, pp. 933-936. ar n92 M.
Arnold, T. Bailey, J. Cowles and J. Cupal.
(1992) Initializing RAM-based
logarithmic processors, J. VLSI Signal
Processing, Vol. 4, pp.
243-252,.
24
References, continued
arn90 M. G. Arnold, et al. (Aug. 1990).
Redundant logarithmic arithmetic, IEEE
Trans. Comput., Vol. 39, pp. 1077-1086. col00
J. N. Coleman, E. I. Chester, C. I. Softley and
J. Kadlec. (July 2000 ) Arithmetic on
the European Logarithmic Microprocessor, IEEE
Trans. Comput.,. Vol. 49, No. 7, pp.
702-715. hen88 H. Henkel. (Feb 1989).
Improved accuracy for the logarithmic number
system," IEEE Trans. Acoust., Speech, Signal
Proc., Vol. ASSP-37, pp.
301-303. kah98 M. Kahrs and K. Branderburg,
eds. (1998) Applications of digital
signal processing to audio and acoustics. Kluwer
Academic Publishers.p. 224. kur91
T. Kurokawa and T. Mizukoshi. (1991). A fast and
simple method for curve drawing--a new
approach using logarithmic number systems,
J. Information Process., Vol. 14, pp. 144-152.
25
References, continued
lew94 D. M. Lewis. (Aug. 1994). Interleaved
memory function interpolators with
application to accurate lns arithmetic units,
IEEE Trans.Comput., Vol. 43, pp.
974-982. lew90 D. M. Lewis. (Nov. 1990). An
architecture for addition and subtraction
of long word length numbers in the logarithmic
number system, IEEE Trans. Comput.,
Vol. 39, pp. 1325-1336. sul93 T.J. Sullivan.
(1993). Estimating the power consumption of
custom CMOS digital signal processing
integrated circuits for both the uniform
and logarithmic number systems, Ph.D.
Dissertation, Washington Univ, St.
Louis, Missouri. pal00 V. Paliouras and T.
Stouraitis. (13-15 Sept. 2000). Logarithmic
number system for low-power arithmetic,
PATMOS 2000 International Workshop on
Power and Timing Modeling, Optimization
and Simulation, Gottingen, Germany, pp.
285-294. pan99 S. Pan et al. (Feb. 1999). A
32b 64-matrix parallel CMOS processor,"
1999 IEEE International Solid-State Circuits
Conference, San Francisco, pp. 15-17.
26
References, continued
swa83 E. E. Swartzlander, D. Chandra, T. Nagle,
and S. A. Starks. (1983).
Sign/logarithm arithmetic for FFT
implementation, IEEE Trans. Comput.,
Vol. C-32, pp. 526-534. tay88 F. J. Taylor, R.
Gill, J. Joseph and J. Radke. (1988). A 20 bit
logarithmic number system processor,
IEEE Trans. Comput., Vol. C-37, pp.
190-199. xil99 Xilinx. (1999). The
programmable logic data book. Xilinx, San Jose,
CA. waz95 M. Wazlowski, A. Smith, R. Citro and
H. Silverman. (1995). Performing
log-scale addition on a distributed memory MIMD
multicomputer with reconfigurable
computing capabilities, Proc. of the
1995 Intl. Conference on Parallel Process. , pp.
III-211 - III-214.