5. Equations of StateSVNA Chapter 3

1
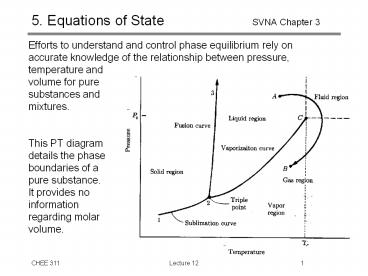
5. Equations of State SVNA Chapter 3

• Efforts to understand and control phase
  equilibrium rely on accurate knowledge of the
  relationship between pressure, temperature and
• volume for pure
• substances and
• mixtures.
• This PT diagram
• details the phase
• boundaries of a
• pure substance.
• It provides no
• information
• regarding molar
• volume.

2
P-V-T Behaviour of a Pure Substance

• The pure component PV-diagram shown here
  describes the relationship between pressure and
  molar volume for the various phases assumed by
  the the substance.

3
PV Diagram for Oxygen
4
Equations of State

• Experimental data exist for a great many
  substances and mixtures over a wide range of
  conditions.
• Tabulated P-V-T data is cumbersome to catalogue
  and use
• Mathematical equations (Equations of State)
  describing P-V-T behaviour are more
  commonly used to represent segments of the phase
  diagram, usually gas-phase behaviour
• Ideal Gas Equation of State
• Applicable to non-polar gases at low pressure
• where V is the molar volume (m3/mole) of the
  substance.
• In terms of compressibility, ZPV/RT, the ideal
  gas EOS gives

5
Equations of State Non-ideal Fluids

• The ideal gas equation applies
• under conditions where molecular interactions are
  negligible and molecular volume need not be
  considered.
• At higher pressures, the compressibility factor,
  Z, is not unity, but takes on a value that is
  different for each substance and various
  mixtures.
• A more complex approach is
• needed to describe PVT behaviour of non-ideal
  fluids

6
Virial Equation of State for Gases

• If our goal to calculate the properties of a gas
  (not a liquid or solid), the PVT behaviour we
  need to examine is relatively simple.
• The product of pressure and molar volume is
  relatively constant, and can be approximated by a
  power series expansion
• from which the compressibility is readily
  determined
• Eq 3.11
• The coefficients B,C,D are called the first,
  second and third virial coefficients,
  respectively, and are specific to a given
  substance at a given temperature.
• These coefficients have a basis in thermodynamic
  theory, but are usually empirical parameters in
  engineering applications.

7
Cubic Equations of State Gases and Liquids

• A need to describe PVT behaviour for both gases
  and liquids over a wide range of conditions using
  an equation of minimal computational complexity
  led to the development of cubic equations of
  state.
• Peng-Robinson (PR) Sauve-Redlich-Kwong
  (SRK)
• in terms of compressibility, Z
• PR-EOS
• SRK-EOS
• where a and b (or A and B) are positive constants
  that are tabulated for the substance of interest,
  or generalized functions of P and T.
• These polynomial equations are cubic in molar
  volume, and are the simplest relationships that
  are capable of representing both liquid and gas
  phase properties.

8
Cubic Equations of State Gases and Liquids

• Given the required equation parameters (a and b
  in the previous cases), the system pressure can
  be calculated for a given temperature and molar
  volume.
• At T gt Tc, the cubic EOS has just one real,
  positive root for V.
• At TltTc there exists only one real, positive root
  at high pressure (molar volume of the liquid
  phase). However, at low pressures the cubic EOS
  can yield three real, positive roots the minimum
  representing the liquid-phase molar volume, and
  the maximum the vapour-phase molar volume.

9
Theorem of Corresponding States

• The virial and cubic equations of state require
  parameters (B, C, a, b, for example) that are
  specific to the substance of interest. In fact,
  the PVT relationships for most non-polar fluids
  is remarkably similar when compared on the basis
  of reduced pressure and temperature.
• Simple fluids aside (argon, xenon, etc), some
  empiricism is required to achieve the required
  degree of accuracy. The three-parameter theorem
  of corresponding states is
• All fluids having the same value of acentric
  factor, ?, when compared at the same Tr and Pr,
  have the same value of Z.
• The advantage of the corresponding states, or
  generalized, approach is that fluid properties
  can be estimated using very little knowledge (Tc,
  Pc and ?) of the substance(s).

10
Theorem of Corresponding States
11
Pitzer Correlations Gases and Liquids

• Pitzer developed and introduced a general
  correlation for the fluid compressibility
  factor.
• 3.54 3.57
• where Zo and Z1 are tabulated functions of
  reduced pressure and temperature.
• This approach is equally suitable for gases and
  liquid, giving it a distinct advantage over the
  simple virial equation of state and most of the
  cubic equations.
• Values of ?, Pc and Tc for a variety of
  substances can be found in Table B.1 of SVNA.
• The Lee/Kesler generalized correlation (found in
  Tables E.1-E.4 of the SVNA) is accurate for
  non-polar, or only slightly polar, gases and
  liquids to about 3 percent.

12
Generalized Virial-Coefficient Correlation Gases

• The tabulated compressibility information that is
  the basis of the generalized Pitzer-type approach
  can be cumbersome (especially in an exam)
• the complex PVT relationship of non-ideal fluids
  is difficult to represent by a simple equation,
  necessitating the use of tables if the
  corresponding states approach is to be accurate.
• SVNA provides a generalized virial EOS
  correlation that allows you to apply the virial
  EOS with coefficients that are based on a
  corresponding states approach (Page 102 SVNA, 6th
  7th ed).
• where
• and

13
PVT Behaviour of Mixtures

• Most equations of state prescribe mixing rules
  that allow you to calculate EOS parameters and
  describe the PVT behaviour of mixtures.
• The Virial EOS,
• the composition dependence of the virial
  coefficient B is
• where y represents the mole fractions in the
  mixture and the indices i and j identify the
  species. Values of Bij are determined using
  generalized correlations and/or formulae
  specifically developed for the mixture of
  interest.
• Mixture behaviour will be examined in greater
  detail later in the course