Problem 9'1

1
Problem 9.1
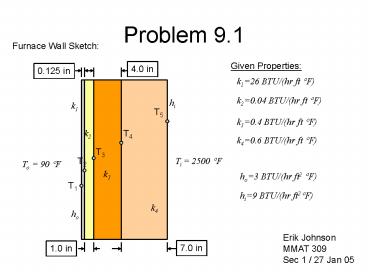
Furnace Wall Sketch
Given Properties
k126 BTU/(hr ft ?F)
k20.04 BTU/(hr ft ?F)
hi
k1
T5
k30.4 BTU/(hr ft ?F)
k2
T4
k40.6 BTU/(hr ft ?F)
T3
T2
Ti 2500 ?F
To 90 ?F
k3
ho3 BTU/(hr ft2 ?F)
T1
hi9 BTU/(hr ft2?F)
k4
ho
Erik Johnson MMAT 309 Sec 1 / 27 Jan 05
2
Problem 9.1
Find a) The Heat Transfer Rate (BTU/
hr-ft2) b) Determine Temps at all interfaces
Solution a) Thermal Circuit Analogy
Ti
To
L2 / k2
L3 / k3
L4 / k4
1 / hi
L1 / k1
1 / ho
3
Problem 9.1
For part b) Again, use thermal circuit analogy
275.25 ?F
275.47 ?F
1434.25 ?F
1897.37 ?F
1959.11 ?F
4
Problem 9.3
Case 1 No Added Insulation
What is the thickness of insulation that reduces
heat loss by 75? 0.25qbeforeqafter
Refractory Brick 0.250 m k0.087 W/mK
Wall Brick 0.050 m k0.087 W/mK
Inside Furnace h55 W/m2K Ti
Outside Furnace h11 W/m2K? To
qbefore(Ti-To)/Arbefore ARbefore1/hi Lrb/krb
Lwb/kwb 1/ho
ARbefore1/(55W/m2K) 0.250m/(0.87W/mK)
0.050m/(0.87W/mK) 1/(11W/m2K) 0.454 m2K/W
Case 2 Added Insulation
Steel Shell 0.025 m k43 W/mK
Refractory Brick 0.250 m k0.87 W/mK
Wall Brick 0.050 m k0.87 W/mK
Outside Furnace h11 W/m2K? To
Insulation L m k0.090 W/mK
Inside Furnace h55 W/m2K Ti
0.25(Ti-To)/ARbefore (Ti-To)/ARafter
0.25/ARbefore 1/ARafter
0.25/(0.454 m2K/W) 1/ARafter
ARafter 1.816 m2K/W
ARafter ARbefore L/kins Lst/kst
1.816 m2K/W 0.454 m2K/W L/(0.090 W/mK)
0.025m/(43W/mK)
L 1.816 m2K/W - 0.454 m2K/W -
0.025m/(43W/mK)/(0.090 W/mK)
L 0.122 m
Trent Molter 1/27/05
5
Problem 9.3 Thermal Resistance Profile
Refractory Brick
Insulation
Inside Furnace
Outside Furnace
Steel Outer Shell
Refractory Brick
Wall Brick
Inside Furnace
Outside Furnace
Wall Brick
Assume Ti1650 K, To300 K

• Observations
• Adding Insulation Significantly Reduces Heat Loss
• With Insulation The Wall Brick Temperature
  Increases By 900K
• The Outer Steel Shell Really Doesnt Help With
  Insulation But May Be
• Necessary to Contain Insulation

Trent Molter 1/27/05
6
Problem 9.5

• Consider steady-state heat conduction through a
  cylindrical wall. The fluid on the inside is at
  590K with a heat transfer coefficient of 23 W m-2
  K-1. The temperature on the outside surface of
  the wall is known and maintained at 420K. The
  heat flow rate through the cylindrical wall is
  200 W per 1m length of the cylinder. If the wall
  has a thermal conductivity of 0.17 W m-1 K-1,
  what are the inside and outside radii of the
  cylindrical wall? The ratio of the outside radius
  to inside radius is 2.

Elizabeth Jordan
7
What we know/assumptions

• No heat flow in the axial or theta direction
• neglect end effects, only radial heat flow.
• heat of fluid inside (590K)
• heat transfer coefficient inside (23 W m-2 K-1)
• outside surface temperature 420K
• heat flow rate (200 W per 1m length of the
  cylinder)
• thermal conductivity of wall (0.17 W m-1 K-1)
• ratio of rin to rout 2

8
Equation to use

• Equation 9.17
• thermal resistance for cylinder
  ln(rout/rin)/2?Lk
• where k is the thermal conductivity
• L is the length
• Q (Tout-Toin)/1/hAinln(rout/rin)/2?Lk

9
Solve equation for Ain and then rin and rout

• Ain 1/(Tin-Tout)/Q-ln(rout/rin)/2?Lk
• with numbers
• Ain 1/(170K/200-ln(2)/2?1.17)
• Ain 1.503m2
• therefore 1.503m2 2?r1(1m)
• rin 0.239m
• rout/0.239m 2 therefore rout 0.478m