Lab2

1
Lab2

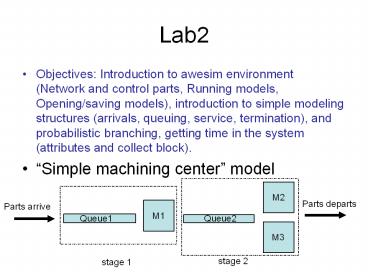
• Objectives Introduction to awesim environment
  (Network and control parts, Running models,
  Opening/saving models), introduction to simple
  modeling structures (arrivals, queuing, service,
  termination), and probabilistic branching,
  getting time in the system (attributes and
  collect block).
• Simple machining center model

M2
Parts departs
Parts arrive
M1
Queue1
Queue2
M3
stage 2
stage 1
2
Lab2

• Simple machining center model

Processing time uniform (6, 10) min Identical
parallel machines
M2
Parts departs
Parts arrive
M1
Queue1
Queue2
M3
Inter arrival times exponential with lambda0.2
part/min
Processing time uniform (2.5, 5.5) min
What are the machine utilization? What are the
queue lengths and times? Simulate it for 30 days
(8 hours working time per day)
3
Lab2

• Embellishment 1 Add an inspection station at the
  end, and assume that 5 of the jobs fail
  inspection and they require rework starting from
  beginning. Ins. time Normal (10,2)
• Embellishment 2 After inspection, 2 requires
  rework in stage 2 only (not from beginning) in
  addition to the 5 in embellishment 1.
• Embellishment 3 Obtain time in the system for
  parts.

4
Lab2

• Assignment 2 Model the following system and
  answer the same questions answered in the lab.

M1
normal(10,2)
Parts arrive
Inspec- tion
Queue2
Queue1
M2
Inter arrival times exponential with mean15
min.
Processing time (identical machines) normal
(mean22.5, std5.7) min
3 rework
Submit a print out of model, control, output, and
your answers.
5
Lab 3

• Objectives To cover Entity dependent processing
  times, routing (conditional branching), and
  naming of attributes to make the model easier to
  read.

6
Lab 3 Simple machining center with inspection

• Embellishment 1 There are two types of parts
  coming to system, type A and type B, as depicted
  in next slide. Type A has to go thorough a
  different machine in the second stage. We want to
  get time in the system separately by item type,
  and overall as well. Use renaming of the
  attributes for arrival time.

7
Lab 3 Simple machining center with inspection
(Embellishment 1)
Gamma(1,2) min
Type A
M4
Queue3
Normal(10,2) min
Type A
M2
Insp.
Type B
Queue4
M1
Queue2
Queue1
M3
Type B
uniform (2.5, 5.5) min
Parts arrive
uniform (4, 6) min (identical machines)
5 rework
Inter arrival times exponential with
lambda0.005 part/min Type A with lambda0.015
part/min Type B
8
Lab3In-lab work-out
Normal (8,2)
Queues are not depicted here
Type B
Ins1
Gamma(2,2)
Type A 40
5 rework
M2
M1
Type B 50
Normal (6,1)
uniform(5.5, 7.5)
Ins2
Inter arrival times gamma(2,5) Run simulation
for 5000 parts Where is the bottleneck?
Type A
3 rework
9
Lab 4

• 1. Entity dependent processing times and entity
  dependent numbering of collect block. 2. Balking
  blocking 3.Different uses of collect block and
  histogram.

10
Lab 4 Simple machining center with inspection

• Embellishment 1 Inspection time depends on job
  type. For type A inspection time is Normal (8,2)
  for type B inspection time is Normal (15,3). Use
  one collect block to get time in the system
  separately by numbering the collect block using
  attribute.
• Embellishment 2 Assume that if there are more
  than 5 parts waiting in queue 1, the arriving
  parts will be sent to another shop for
  processing. Obtain how often this happens. We
  would like to obtain histogram of time in the
  system as well.

11
Lab4In-lab work-out Maintenance shop

• Maintenance facility of a large manufacturer
  performs two operations in series . The units
  that are maintained are heavy, and the space in
  the shop is available only for 8 units including
  the units being worked on. The proposed design
  allocates 4 units for first queue, 2 units for
  second queue. Company subcontracts incoming units
  if the maintenance shop is full. If the second
  queue is full, the first workstation is blocked.

12
Lab4In-lab work-out Maintenance shop

• Arrivals exponential with mean 0.4 time units
• Processing times first station exponential with
  mean 0.25, second station exponential with mean
  0.5
• No significant time for transfer from first
  station to next.
• Evaluate proposed design for 300 time units in
  terms of
• utilizations, time in the system, time between
  the subcontracting, queue lengths, fraction of
  time work station 1 is blocked (The correct
  answers avr. tims 2.7, time btw balk 1.5)
• Any better design???

13
LAB 5

• Objective 1. To complete the in-lab workout
  started in previous lab and the embellishment of
  it. 2. To learn how to do batch arrivals, use of
  NQ(), multiple runs, the ranking in queues,
  flexible use of attributes.

14
LAB 5 In-lab workout

• Complete the model for the problem described in
  previous lab.
• Embellishment Assume that there are two types of
  units that comes to the system, and second stage
  operation time depends on type of unit as
  follows Type A Gamma(0.5,0.6) and Type B
  Gamma(1, 0.8). Use one collect block to get time
  in the system separately by type. Produce a
  histogram of time in the system for both types.

15
LAB 5TV inspection station

• Consider the following TV inspection adjustment
  station where we have two inspectors and one
  adjuster. TV sets arrive in sets of two TVs with
  uniform btw 7 and 15.

Incoming TVs join the shorter queue. The
processing time in inspection stations are
uniform(6, 12). Adjustment takes shifted gamma(2,
2) with min 1.5. Obtain time in the system based
on 1000 parts leaving the system. Do 50 runs.
16
LAB 5TV inspection station

• Embellishment Assume that in all queues, we use
  shortest process time first rule. After
  adjustment, make sure the TVs go back to the same
  inspector queue that they came from.

17
LAB 5 Assignment 3TV inspection station

• Embellishment of TV inspection model There are
  two types of TV sets. 40 type A and 60 type B.
  Adjustment time depends on the type of TV set as
  follows Type A gamma(2, 2) with min 1.5 and Type
  B gamma(1.8, 2.5) with min 1. Also assume that if
  a TV is adjusted before, it passes the inspection
  95 of the time. Change ranking rule to longest
  processing time first. Do your simulation for 40
  runs, obtain time in the system by type.