Multivariate Applications in Ecology

1
(No Transcript)
2
,1 ,2 ,3 Beaver1_5_2005
-0.11536473 -0.024133621 0.128454443 Beaver1_6_20
05 0.05044035 0.253409935 0.044058328 Big1_2_
2006 -0.12847566 -0.262919513
-0.292431542 Big2_1_2006 -0.07243953
-0.261425521 -0.058826529 Big2_1_2006b
-0.01373644 -0.242757242 -0.039883862 Big2_10_2005
-0.16424322 -0.385294715 -0.325273118 Big2_11
_2005 -0.28889848 -0.264885907
0.075858409 Big2_2_2006 -0.13500749
-0.361974771 -0.058301161 Big2_5_2005
-0.10057629 -0.358418918 -0.143062037 Big2_6_2005
-0.02848600 -0.298375256 -0.320120636 Big2_7_
2005 -0.09964887 -0.294943951
-0.262597167 Big2_8_2005 -0.21958022
-0.324787308 -0.088282460 Big2_9_2005
-0.12921246 -0.295372136 -0.275017445 Bouie1_3_200
6 -0.08354853 0.297500631 -0.024330967 Bouie1_
7_2005 -0.24721861 -0.073153351 0.248429945
eig 1 5.405133 3.801171 2.209406 GOF 1
0.3914725 0.4314720
3
R0.81
4
(No Transcript)
5
(No Transcript)
6
(No Transcript)
7
Principle Components Analysis (PCA)

• First and most basic eigenvalue based ordination
• Works with the original dataset, not a distance
  matrix
• Works best with linear relationships among
  variables (species), thus some data
  transformations usually required with species data

8
Principle Components Analysis (PCA)
Two dimensional regression best fit line
through points describes the relationship,
explains some proportion of variance. PCA is
similar but in multivariate space. Best fit line
in multiple dimensions component. By
definition passes through centroid.
9
Dust bunny distributions
PCA works best with data that are multivariate
normal with linear relationships Species data
tends not to be structured this way.
10
Shared Zeroes and Outliers
Shared zero data among species will lead to a
false high positive relationship. A single
large outlier can define the linear relationship
among two variables.
11
Principle Components Analysis (PCA)

• Eigenvalue based approach
• Code
• prin_complt-prcomp(community, scaleFALSE,
  tol0.5)
• Options
• Scale rescale data automatically to have unit
  variance ( 1SD per variable)
• Center center each variable around 0
• Tol tolerance level for which components are
  accepted. Tol0.5 means ignore components whose
  eigenvalues are half or less than component 1.
• Other functions
• Pca from labdsv package
• Princomp use if you want to use the covariance
  matrix

12
Output

• Principle Components are formed to express as
  much variability as possible, are orthogonal, and
  each explains less variation than the previous.
• Eigenvalues - percent variation explained by
  each component
• Eigenvectors coefficient of linear equation for
  each component.
• Projections each sample is projected into
  ordination space using the original data and the
  eigenvectors.
• Function Predict project new data onto existing
  ordination space. How would this sample fit in
  the ordination without actually changing the
  ordination?

13
Biplot species and samples in ordination space
What to present Ordination - Sample Scores
Loadings Percent variance accounted for
Projection of new samples into ordination
space -
Species 2
Species 1
14
Data Assumptions

• Often helpful to look at scatter plots of data
  first
• Common transformations eliminate rare species,
  log transform, scale data etc.

15
How many axes, which to use?

• By definition, axes of variables (species)
• By definition, all axes account for 100 of
  variance
• First axis accounts for most variance, decreases
  from there.
• How many to use?
• Descriptive (2D plot)
• Analytical (non-random axis, Monte Carlo
  determination)

16
Dust bunnies, hockey sticks and global warming
17
(No Transcript)
18
(No Transcript)
19
How many axes
20
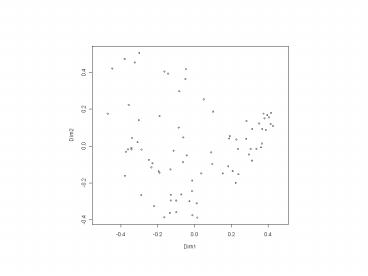
Example PCA on simple dataset
21
Importance of components
PC1 PC2 PC3 PC4 PC5 PC6 PC7
PC8 PC9 Standard deviation 2.137 1.797
1.012 0.9757 0.31297 0.23985 0.16906 0.16340
0.10108 Proportion of Variance 0.457 0.323 0.102
0.0952 0.00979 0.00575 0.00286 0.00267
0.00102 Cumulative Proportion 0.457 0.780 0.882
0.9774 0.98723 0.99298 0.99584 0.99851 0.99953
PC10 Standard deviation
0.06857 Proportion of Variance
0.00047 Cumulative Proportion 1.00000 gt
sum(prin_compsdev) 1 6.977327
Recall these are actually square roots. Square
them and they add to 10.
2.1372 / 10 0.457
PC1 PC2 PC3 PC4 PC5
PC6 sp1 -0.3348192 0.23876063 -0.4989338
0.1944896 0.2884486 0.2426002 sp2 -0.3957956
0.07982772 -0.1283219 0.4862885 0.2842866
-0.1867800 sp3 -0.3801118 -0.14813118 0.2546030
0.4393928 -0.2649294 -0.3579026 sp4 -0.2764337
-0.37688556 0.3757525 0.1625829 -0.2653249
0.3083082 sp5 -0.1016927 -0.52214493 0.1690737
-0.0787275 0.4420335 0.4279137 sp6 0.1016927
-0.52214493 -0.1690737 -0.0787275 0.4420335
-0.4279137 sp7 0.2764337 -0.37688556 -0.3757525
0.1625829 -0.2653249 -0.3083082 sp8 0.3801118
-0.14813118 -0.2546030 0.4393928 -0.2649294
0.3579026 sp9 0.3957956 0.07982772 0.1283219
0.4862885 0.2842866 0.1867800 sp10 0.3348192
0.23876063 0.4989338 0.1944896 0.2884486
-0.2426002 PC7 PC8
PC9 PC10 sp1 -0.48264944 0.28151312
-0.02926947 -0.2983522 sp2 0.16724718
-0.53979178 -0.02484725 0.3851760 sp3
0.20300091 0.33145859 0.22963732 -0.4166463 sp4
-0.44006188 0.02657036 -0.43201217
0.2597543 sp5 0.06491585 -0.13712919
0.50907574 -0.1468297 sp6 0.06491585
0.13712919 -0.50907574 -0.1468297
22
(No Transcript)
23
(No Transcript)
24
Similar dataset, species linearly related
25
Importance of components
PC1 PC2 PC3 PC4 PC5 PC6
PC7 PC8 Standard deviation 3.151 0.25597
0.06433 0.02807 0.01610 0.01089 0.00828
0.00688 Proportion of Variance 0.993 0.00655
0.00041 0.00008 0.00003 0.00001 0.00001
0.00000 Cumulative Proportion 0.993 0.99945
0.99987 0.99995 0.99997 0.99998 0.99999 1.00000
PC9 PC10 Standard
deviation 0.00606 4.77e-17 Proportion of
Variance 0.00000 0.00e00 Cumulative Proportion
1.00000 1.00e00
Analysis worked much better, nearly all
variation explained by the first axis.
26
(No Transcript)