Classification Problem 2Category Linearly Separable Case

1
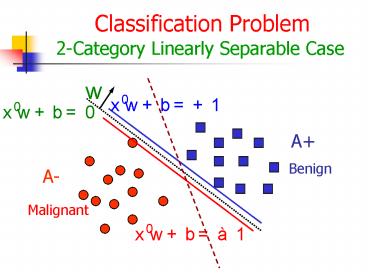
Classification Problem2-Category Linearly
Separable Case
Benign
Malignant
2
Support Vector MachinesMaximizing the Margin
between Bounding Planes
A
A-
3
Algebra of the Classification Problem2-Category
Linearly Separable Case
4
Support Vector Classification
(Linearly Separable Case)
Let
be a linearly
separable training sample and represented by
matrices
5
Support Vector Classification
(Linearly Separable Case, Primal)
The hyperplane
that solves the
minimization problem
realizes the maximal margin hyperplane with
geometric margin
6
Support Vector Classification
(Linearly Separable Case, Dual Form)
The dual problem of previous MP
Dont forget
7
Dual Representation of SVM
(Key of Kernel Methods
)
The hypothesis is determined by
8
Compute the Geometric Margin via Dual Solution

• The geometric margin

and

• Use KKT again (in dual)!

9
Soft Margin SVM
(Nonseparable Case)

• If data are not linearly separable

• Primal problem is infeasible

• Dual problem is unbounded above

• Introduce the slack variable for each training
• point

• The inequality system is always feasible

e.g.
10
(No Transcript)
11
Two Different Measures of Training Error
2-Norm Soft Margin
1-Norm Soft Margin
12
2-Norm Soft Margin Dual Formulation
The Lagrangian for 2-norm soft margin
The partial derivatives with respect to
primal variables equal zeros
13
Dual Maximization Problem For 2-Norm Soft Margin
Dual

• The corresponding KKT complementarity

• Use above conditions to find

14
Linear Machine in Feature Space
Make it in the dual form
15
Kernel Represent Inner Product in Feature Space
Definition A kernel is a function
such that
where
The classifier will become
16
Introduce Kernel into Dual Formulation
Let
be a linearly
separable training sample in the feature space
implicitly defined by the kernel
.
The SV classifier is determined by
that
solves
17
Kernel Technique
Based on Mercers Condition (1909)

• The value of kernel function represents the
  inner product in feature space
• Kernel functions merge two steps
• 1. map input data from input space to
• feature space (might be infinite
  dim.)
• 2. do inner product in the feature space

18
Mercers Conditions Guarantees the Convexity of
QP
19
Introduce Kernel in Dual Formulation For 2-Norm
Soft Margin

• The feature space implicitly defined by

• Suppose

solves the QP problem

• Then the decision rule is defined by

• Use above conditions to find

20
Introduce Kernel in Dual Formulation for 2-Norm
Soft Margin

is chosen so that
for any
with
Because
and
21
Geometric Margin in Feature Space for 2-Norm Soft
Margin

• The geometric margin in the feature space
• is defined by

• Why

22
Discussion about C for 2-Norm Soft Margin

• Larger C will give you a smaller margin in
• the feature space

• The only difference between hard margin
• and 2-norm soft margin is the objective
• function in the optimization problem