Density

1
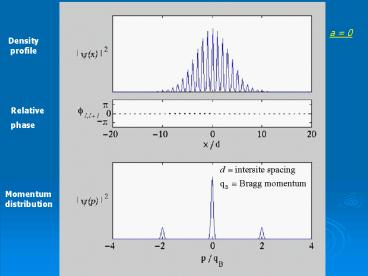
a 0
Density profile
Relative phase
Momentum distribution
2
Condensate diffraction from an optical grating
LENS, Florence
3
Energy and quasi-momentum are conserved
4
agt 0
5
Array of weakly coupled BEC
6
BEC expanding in a 1D optical lattice
A. Trombettoni and A. Smerzi, PRL 86, 2353 (2000)
7
Array of Josephson junctions driven by a
harmonic external field
8
Oscillations of the three peaks of the
interferogram. Blue circles no periodic
potential
The array is governed by a pendulum equation
F.S. Cataliotti, S. Burger, C. Fort, P.
Maddaloni, F. Minardi, A. Trombettoni, A.
Smerzi, M. Inguscio, Science 293, 843 (2001)
9
Small amplitude pendulum oscillations
Triangles GPE stars variational calculation of
K Circles experimental results
Relation between the oscillation frequency and
the tunneling rate
10
Breakdown of Josephson oscillations
The interwell phase coherence breaks down for a
large initial displacement of the BEC center of
mass
11
Questions

• 1) Why the interaction can break the inter-well
  phase coherence
• of a condensate at rest confined in a
  periodic potential ?
• 2) Why a large velocity of the BEC center of
  mass can break the inter-well phase coherence of
  a condensate confined in a periodic potential and
  driven by a harmonic field ?

Which are the transport properties of BEC in
periodic potentials ?
12
(No Transcript)
13
Nonlinear tight-binding approximation
Replace in GPE and integrate over spatial degrees
of freedom Dynamical equations for
atom numbers and phases in each well
14
The discrete nonlinear equation (DNL)
15
The shape and effective dimensionality of each
condensate depends on a balance between the local
interaction chemical potential and trapping
frequencies
Array of weakly coupled pancakes, cigars,
ellipsoidal condensates
16
Bloch energies effective masses
Effective masses depend on the height of the
inter-well barriers and on the density
17
Bloch states
Bloch energy and chemical potential
Masses
Effective masses depend on the height of the
inter-well barriers and on the density
18
Bloch energies, effective masses velocities
How/which mass and velocity enter in the dynamics
?
19
Bogoliubov spectrum

• Replace in the DNL
• After linearization, retrieve the dispersion
  relation

20
Bogoliubov spectrum
21
Sound
22
Dynamical instability
The amplitude of the perturbation modes grows
exponentially fast, dissipating the energy of the
large amplitude wave-packet
No dynamical instabilities
New mechanism for the breakdown of superfluidity
of a BEC in a periodic potential
23
Energetic instability
cfr. with the free (V0) limit
Landau criterion for breakdown of superfluidity
24
Landau criterion for Superfluidity

• Gross-Pitaevskii equation with a defect
• Vdef V0 ?(t)d(x)
• Expansion of the wave-function in terms of the
  quasi-particle basis

25
Orthogonality and Symmetry conditions
with up and vp satisfying the Bogoliubov-De
Gennes equations
Bogoliubov frequency
26
Quasi-particle amplitude

• For small defects the quasi-particles occupations
  are small compared to the condensate mode

Landau critical velocity vcc
27
Landau criterion for Superfluidity
Normal fluid The presence of the defect causes
dissipation and quasi-particles creation growing
of the thermal fraction.
Laser beam
BEC
Critical velocity
Superfluid the defect does not affect the motion
of the condensate which moves without
dissipations.
C.Raman et al., Phys. Rev. Lett., Vol. 83, No. 13
28
Energetic vs. dynamical instability
EI always sets in before the DI
EI
DI EI
stable
DI EI
stable
EI
29
Breakdown of superfluidity for a BEC driven by
a harmonic field
Quasi-momentum vs. time for three different
initial displacements 40, 80, 90 sites
Density at t0,20,40 ms as a function of
the Position. Initial displacements 50, 120
sites
A. Smerzi, A. Trombettoni, P.G. Kevrekidis, A.R.
Bishop, PRL 89, 170402 (2002)
30
Newtonian Dynamics
Dynamical variational principle
31
Newtonian Dynamics
Group velocity
Effective force
32
(No Transcript)
33
Bloch oscillations

• Atoms are condensed in the optical and magnetic
  fields.
• The harmonic confinement is instantaneously
  removed along the x direction.
• 3. A linear potential is superimposed to the
  system

Green line a0 Blue line agt0
34
(No Transcript)
35
Damping of Bloch Oscillations
Solid line Analytical Dashed line Numerical
A. Trombettoni and A. Smerzi, PRL 86, 2353 (2000)
36
(No Transcript)
37
Quantum dynamics
Two-mode boson-Hubbard model
38
Number state representation
39
Coherent state representation
40
phase state representation
41
(No Transcript)
42
Two-modes base
43
Fock states can be seen as a superposition of
phase states with random phase
44
(No Transcript)
45
(No Transcript)
46
(No Transcript)
47
The lowest N1 eigenenergies are exactly the N1
eigenenergies of the two-mode boson-Hubbard
Hamiltonian
48
(No Transcript)
49
Quantum phase model
The QPM describes the Fock regime and part of
the Josephson regime
50
Variational dynamics
51
(No Transcript)
52
(No Transcript)
53
(No Transcript)
54
(No Transcript)
55
Classical limit
56
Numerical solutions