Example: 8Puzzle

1
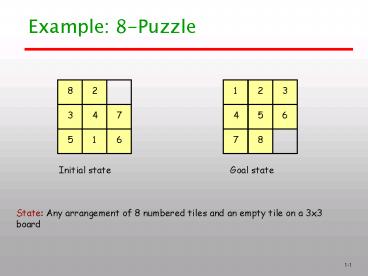
Example 8-Puzzle
State Any arrangement of 8 numbered tiles and an
empty tile on a 3x3 board
2
How big is the space of the puzzle

• 8-puzzle ? ?? states

3
How big is the space of the puzzle?

• 8-puzzle ? 9! 362,880 states
• 15-puzzle ? 16! 2.09 x 1013 states
• 24-puzzle ? 25! 1025 states
• But only half of these states are reachable from
  any given state(but you may not know that in
  advance)

4
8-Puzzle Successor Function
Search is about the exploration of alternatives
5
Heuristic Function

• Function h(N) that estimate the cost of the
  cheapest path from node N to goal node.
• Example 8-puzzle

h(N) number of misplaced tiles 6
goal
N
6
Heuristic Function

• Function h(N) that estimate the cost of the
  cheapest path from node N to goal node.
• Example 8-puzzle

h(N) sum of the distances of every
tile to its goal position 2 3 0 1
3 0 3 1 13
goal
N
7
Distances
3
3
Current State
2 spaces

• The Manhattan Distance (not including the blank)

8
3 spaces
Goal State
8
1
3 spaces
1
Total 8
8
Beginning of a Heuristic Search
9
Search Tree After Two Passes
10
Search Tree After Three Passes
11
Complete Search Tree
12
How machine check the syntax?

• Syntax processing is divided into two phases
• Scanning
• collects characters into tokens
• Example 3.14
• Parsing
• determines syntactic structure

13
Lexical Analyzer (Scanner)
14
How to design the grammar?

• Earlier year, the syntax grammar is difficult to
  design.
• Good news, good ideas
• Finite state machine
• Scanner has ability to define the token and
  analyze the different language.

15
Languages

• A language is a set of strings
• String A sequence of letters
• Examples cat, dog, house,
• Defined over an alphabet

16
Alphabets and Strings

• We will use small alphabets
• Strings

17
Defining Tokens
18
Regular Expression Examples
19
Properties

• concatenation and alternation are associative
• eg, ABC means (AB)C and is equivalent to A(BC)
• alternation is commutative
• eg, A B B A
• repetition is idempotent
• eg, A A
• concatenation distributes over alternation
• eg, (a b)c ac bc

20
The Operation

• the set of all possible strings from
• alphabet

21
The Operation
the set of all possible strings from
alphabet except
(e)
(e)
22
Another Example

• An infinite language

23
Operations on Languages

• The usual set operations
• Complement

24
Reverse

• Definition
• Examples

25
Concatenation

• Definition
• Example

26
Examples of RE Around

• Phones number consider [phone]
• digit ? -, (, )
• exchange digital 3 times
• phone digit 4 times
• area digital 2 times
• phone_number '(' area ')' exchange '-' phone
• Email address student_at_nccu.edu.tw
• Try it

27
Finite Automata State Graphs

• A state

• The start state

• An accepting state

• A transition

28
A Simple Example

• A finite automaton that accepts only 1

1
29
Another Simple Example

• A finite automaton accepting any number of 1s
  followed by a single 0
• Alphabet 0,1

1
0
30
And Another Example

• Alphabet 0,1
• What language does this recognize?

0
1
0
0
1
1
31
And Another Example

• Alphabet still 0, 1
• The operation of the automaton is not completely
  defined by the input
• On input 11 the automaton could be in either
  state

1
1
32
Acceptance of NFAs

• An NFA can be in multiple states

• Input

1
0
1

• Rule NFA accepts if at least one of its current
  states is a final state

33
Transition Graph
Abba -Finite Accepter

initial state
final state accept
transition
state
34
Initial Configuration
Input String

35
Reading the Input
36
Reading the Input
37
Reading the Input
38
Reading the Input
39
Reading the Input
Input finished
Output accept
40
Rejection

41
Rejection
42
Rejection
43
Rejection
44
Rejection
Input finished
Output reject
45
Another Example
46
Another Example
47
Another Example
48
Another Example
49
Another Example
Input finished
Output accept
50
Rejection
51
Rejection
52
Rejection
53
Rejection
54
Rejection
Input finished
Output reject
55
Transition Function

56
More Examples

trap state
accept
57
The simple example
??? ??
B
E
G
I
N
6
0
1
2
3
4
5
??? ??
N
D
E
10
7
8
9
l
??? ??
S
E
14
11
12
13
??? ??
F
I
17
15
16
??? ??
H
E
N
T
22
18
19
20
21
58
The DFA of a Scanner

• for-keyword for
• identifier a-za-z0-9

59
Nondeterministic Finite Accepter (NFA)
Alphabet
Two choices
No transition
No transition
60
First Choice
61
First Choice
62
First Choice
63
First Choice
All input is consumed
accept
64
Second Choice
65
Second Choice
66
Second Choice
No transition the automaton hangs
67
Second Choice
Input cannot be consumed
reject
68
Lambda Transitions
69
Lambda Transitions
70
Lambda Transitions
71
Lambda Transitions
(read head doesnt move)
72
Lambda Transitions
73
Lambda Transitions
all input is consumed
accept
String is accepted
74
Rejection Example
75
Rejection Example
76
Rejection Example
(read head doesnt move)
77
Rejection Example
No transition the automaton hangs
78
Rejection Example
Input cannot be consumed
reject
String is rejected
79
Lambda Transitions
Language accepted
80
Language accepted
81
Example

• (a b)(abb ab)

82
Example
83
Try it!!
Ex. Given
a b c
1
3
2
4
d
b c
6
5
7

• Initially, two sets 1, 2, 3, 5, 6, 4, 7.
• 1, 2, 3, 5, 6 splits 1, 2, 5, 3, 6 on c.
• 1, 2, 5 splits 1, 2, 5 on b.
• so finally we have

ad b c
2,5
3,6
4,7
1
84
Example

• regular languages recognized by finite automata
• (A , X , d)
• A states q1,q2
• X input alphabet 0,1
• d transition function

85
Vending Machine Example

• Suppose a certain vending machine accepts
  nickels, dimes, and quarters.
• If gt30 is deposited, change isimmediately
  returned.
• If the coke button is pressed,the machine
  drops a coke.
• Can then accept a new payment.

Ignore any otherbuttons, bills,out of
change,etc.
86
Modeling the Machine

• Input symbol set I nickel, dime, quarter,
  button
• We could add nothing as an additional input
  symbol if we want.
• Representing no input at a given time.
• Output symbol set O ?, 5, 10, 15, 20,
  25, coke.
• State set S 0, 5, 10, 15, 20, 25, 30.
• Representing how much money has been taken.

87
Transition Function Table
88
Transition Function Table cont.
89
Another Format State Table
Each entryshowsnew state,output symbol
90
Directed-Graph State Diagram

• As you can see, these can get kind of busy.

q,5
d,5
q
q
q,20
d
d
d
n
n
n
n
n
n
0
5
10
15
20
25
30
n,5
b
b
b
b
b
b
d,10
q,25
q,15
b,coke
q,10
91
Stack FSM Thief 3
92
Case Study Robocode

• First determine what states are needed
• Attack, Evade, Search, etc.
• Code up the FSM transition function.
• Include an error state that is noticeable.
• Setup debugging.
• Verbosity levels are a must.

93
Case Study Robocode
Defend
Search
Implement and test each state separately.
A test bot AI might help test single behaviors.
(see Target bot)
Attack
94
RE is good for programming concept

• If the boss of the company want you to extract
  the special patterns from the large amount of the
  data, How to do it!
• Using your eyes to see the formal rules
• RE will help you to do the good program
• Finite state machine will help you to do the
  logic design and cover all possible situation
• RE can help us do
• Using grammar to handle the special patterns
• Help you to do the concept mining
• Knowledge extraction for the rules