Chapter 2: The Theory of Interest
1 / 77
Title:
Chapter 2: The Theory of Interest
Description:
... card interest a good idea? ... (reverse the Future Value Idea) r. Future Value Idea: A A' = (1 r) ... Don't forget the 'net' idea. Apples & Oranges Warning for ... –
Number of Views:101
Avg rating:3.0/5.0
Title: Chapter 2: The Theory of Interest
1
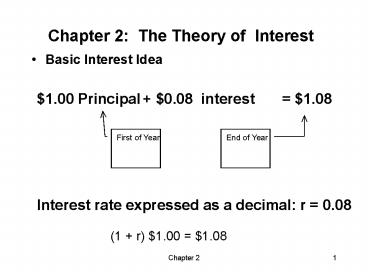
Chapter 2 The Theory of Interest
- Basic Interest Idea
1.00 Principal
0.08 interest
1.08
First of Year
End of Year
Interest rate expressed as a decimal r 0.08
(1 r) 1.00 1.08
2
Simple Interest Rate
3
Simple Interest Rate (Contd)
- If the proportional rule holds for fractional
years, after any time t (measured in years) then - V (1 r t) A
- Certificates of Deposit sometimes pay simple
interest.
4
Compound Interest Rate
5
Compound Interest Rate (Contd)
- Question. Would you rather have simple interest,
or compound interest? - Guesses Suppose you can get 10 compound
interest yearly on a 2,000 IRA. How much would
it be worth after 10, 20, 30 or 40 years?
6
Seven-Ten Rule
- (1.1)7 1.949. Money invested at 10 per year
doubles in about 7 years. - (1.07)10 1.967. Money invested at 7 per year
doubles in about 10 years. - Twenty-Eighty Rule
7
Compound Interest (Compound.xls)
8
Compound Versus Simple Interest
- Compound interest is said to exhibit geometric
growth. - Given the same annual rate, compound interest
always gives a greater value than simple
interest, since simple interest grows linearly.
9
Effective Interest Rate
- Compounding at other intervals than yearly e.g.,
daily, monthly, quarterly. - Quarterly compounding of an interest rate r for a
year applied to an amount A results in (1r/4)4 A
in a year. In this case, r satisfying 1 r
(1r/4)4 is called the effective interest rate
and r is nominal rate - Example r 0.08, r/4 0.02, 1 r (1.02)4
1.0824, r 0.0824 is the effective interest
rate. Note r gt r.
10
Continuous Compounding
- useful for modeling simplifications
- If an interest rate r is compounded m times per
year, after m periods, the result is - (1 r/m)m
- Further,
- lim m-gt ? (1 r/m)m er , where e ? 2.7818
- Example e0.08 1.0833, compared with (1.02)4
1.0824
11
Continuous Compounding (Contd)
- Continuous Compounding for t years gives
- (1 r/m)m t -gt er t
12
Debt
- You can also be on the paying end of compound
interest. It works both ways. - If you borrow money and do not make payments
after one year your debt is - (1r/12)12
(interest is charged monthly) - Interest rates change regularly and depend upon
the borrowing period - Question. Is paying credit card interest a good
idea? - (explain credit card tricks with grace period
and compound interest)
13
Credit Card Example (CrdCard.xls)
14
Present Value
- Present Value (reverse the Future Value Idea)
- r
- Future Value Idea A ? A (1r) A
-
d1 - Present Value Idea A 1/(1r) A d1 A ?
A - Example. If 100 is worth 108 in one year, then
the present value of that 108 is 100.
15
Example
- If 100 is worth 108 in one year, then the
present value of that 108 is 100. - Receiving 108 in one year is no different than
putting 100 in a bank and letting it earn 8
interest for one year. - If you owe 108 in one year, its present value is
just 100, since you could put 100 in the bank
today at 8 interest and have the money to pay
the debt in a year. - If you owe an amount A in one year, you could
put A/(1r) in the bank today at interest rate r
and have the money to pay the loan in a year.
16
Discounting
- (1-year) Discount Factor d1 1/(1r).
- Example r 0.08, d1 1/(10.08) ? 0.926
- Discounting the process of evaluating future
obligations as an equivalent present value. - Note, at 8, in two years
- 100 ? 108 ? 116.64
17
k-Period Discounting
- At 8 a year, the present value of a debt of
116.64 due in two years is 100. - More generally, with compounding of m equal
periods per year, and in k periods - dk 1/1 (r/m)k (k-period discount
factor) - Present value of a payment A to be received k
periods in the future is dk A.
18
PV FV of Streams
- Ideal Bank A bank which does the following
- applies the same rate of interest to both
deposits and loans - has no service charges or transactions fees
- its interest rate does not depend on the size of
the principal - separate transactions in an account are
completely additive in their effect on future
balances.
19
PV FV of Streams (Contd)
- Example of Ideal Bank
- 2-year CD offers same rate as a loan payable in 2
years. - Rates for 1-year and 2-year CDs need NOT be the
same.
20
Constant Ideal Bank
- Constant ideal bank is an ideal bank with
- an interest rate independent of the length of
time for which it applies - interest compounded according to normal rules
(ones we have presented for compound interest) - A constant ideal bank is the reference point
used to describe the outside financial market
the public market for money.
21
FV of Cash Flow Stream
- Cash Flow Stream (x0,x1, , xn)
- We have a fixed time cycle for compounding
(e.g., yearly), a period is the length of this
cycle. Cash flows occur at the end of each
period (some can be zero). We deposit each cash
flow in a constant ideal bank, paying r per
period.
22
FV of Cash Flow Stream (Contd)
- x0 grows to x0 (1r)n
- x1 grows to x1 (1r)n-1
- x2 grows to x2 (1r)n-2
- xn grows to xn (1r)n-n
- Future value of cash flow stream with interest
rate r per period is - FV x0 (1r)n x1 (1r)n-1 x2 (1r)n-2
xn
23
FV Example
- 2K invest in IRA each year for n years
24
FV Example (Contd)
25
PV of Cash Flow Stream
- Cash Flow Stream (x0,x1, , xn)
- We have a fixed time cycle for compounding (e.g.,
yearly), a period is the length of this cycle.
Cash flows occur at the end of each period (some
can be zero). We deposit each cash flow in a
constant ideal bank, paying r per period.
26
PV of Cash Flow Stream (Contd)
- x0 is now worth x0
- x1 is now worth x1 /(1r)1
- x2 is now worth x2 /(1r)2
- xn is now worth xn /(1r)n
- Present Value of cash flow stream with interest
rate r per period is - PV x0 x1 /(1r)1 x2 /(1r)2 xn/(1r)n
27
Example
- Stream (-2,1,1,1), r 0.10
- PV -2 1/(1.10) 1/(1.10)2 1/(1.10)3
- -2 0.9090 0.8264 0.7513 ? 0.4869.
- This present payment amount of 0.487 is
equivalent to the entire stream.
28
Relation of PV and FV
- Question
- FV x0 (1r)n x1 (1r)n-1 x2 (1r)n-2
xn - PV x0 x1 /(1r)1 x2 /(1r)2
xn/(1r)n - What do you get if you multiply PV by (1r)n ?
- Conclusion For a cash flow stream with rate r,
29
Relation of PV and FV (Contd)
- The FV and PV functions are both in Excel.
- Example Stream (-2,1,1,1), r 0.10.
- PV 0.487, FV 0.648,
- PV FV/(1.1)3 0.487.
- Both PV and FV are equivalent ways to think about
the stream.
30
Frequent and Continuous Compounding
- Cash Flow Stream (x0,x1, , xn)
- r nominal annual interest rate, interest
compounded at m equally spaced periods per year - PV x0 x1 /1(r/m)1 x2 /1(r/m)2
xn/1(r/m)n - Continuous Compounding at times t0, t1, , tn and
stream (x(t0),x(t1), , x(tn)) - PV x(t0)e-rt0 x(t1)e-rt1 x(tn) e-rtn
31
Equivalent Cash Streams
- Definition X and Y are equivalent if both
streams have the same PV, evaluated at the banks
interest rate r - Ideal bank can transform X to Y (Y to X)
- Example. With r 0.1, the following are
equivalent - (1,0,0), (0,0,1.21), (0,1.1,0), (a,b,c) for any
a, b, c with - 1 a b/(1.1) c/(1.1)2
32
Internal Rate of Return
- Motivating Example. An ideal bank offers you the
following - Deal 1. Invest 2,000 today. At the end of
years 1, 2, and 3 get 100, 100, and 500 in
interest at the end of year 4, get 2,200 in
principal and interest. - Question. Is this a good deal?
- Approach find out the implicit interest rate you
would be receiving that is, solve for - 2000 100 /(1r)1 100 /(1r)2 500/(1r)3
2200/(1r)4 - Solution r 10.7844 . This is the interest
rate for the PV of your payments to be 2,000.
33
Internal Rate of Return (Contd)
- Deal 2 At the end of years 1, 2, and 3 get 100,
100, and 100 in interest at the end of year 4,
get 2,000 in principal only. - We find r for which
- 2000 100 /(1r)1 100 /(1r)2 100/(1r)3
2000/(1r)4 - Solution r 3.8194.
- Which deal would you prefer?
- Would either deal be attractive?
34
Internal Rate of Return (Contd)
- How do we even know that the following equation
has a solution? - 2000 100 /(1r)1 100 /(1r)2
- 500/(1r)3 2200/(1r)4
- Let c 1/(1r). Rewrite the equation as
- -2000 100 c 100 c2 500 c3 2200 c4 0.
- This is now a 4th degree polynomial in c. We
know, from algebra, that an nth degree polynomial
has exactly n roots. However, we need to be sure
the roots are real numbers (and not imaginary).
We would also like them to be positive.
35
Internal Rate of Return (Contd)
- If c 0, f(c) -2000 lt 0. For c sufficiently
large, f(c) gt 0. Further, f is a continuous
function, and strictly increasing. The c value,
say c0, where f(c0) 0, (where the graph
intersects the origin) is therefore the only
real, positive root. Also f(1) 900 gt 0, so the
root satisfies c0 lt 1.
36
Internal Rate of Return (Contd)
- Observation. The number r satisfying
- 2000 100 /(1r)1 100 /(1r)2 500/(1r)3
2200/(1r)4 - i.e.,
- 0 -2000100 /(1r)1 100 /(1r)2 500/(1r)3
2200/(1r)4 - is also the number r for which the cash flow
stream - (-2000,100,100,500,2200) has PV 0, since
- PV x0 x1 /(1r)1 x2 /(1r)2 xn/(1r)n
37
Internal Rate of Return (Contd)
- Let (x0,x1, , xn) be a cash flow stream. The
internal rate of return (IRR) of this stream is a
number r satisfying - 0 x0 x1 /(1r)1 x2 /(1r)2 xn/(1r)n
- Remark. We use the word internal because the
rate of return depends only on the stream. It is
not defined with reference to the financial
world. It is the rate an ideal bank would have
to apply to generate the given stream from an
initial balance of zero.
38
IRR in EXCEL
39
Main Theorem of IRR
- Suppose the cash flow stream (x0,x1, , xn) has
- x0 lt 0, and xk ? 0 for k 1, , n with at
least one of x1, , xn positive. Then there is a
unique positive root to the equation - f(c) x0 x1 c x2 c2 xn cn
- Further, if x0 xn gt 0 (the total return
then exceeds the initial investment, x1 xn
gt -x0), then the corresponding IRR r (1/c) 1
is positive.
40
Proof of Main Theorem of IRR
- f(0) x0 x1 0 x2 02 xn 0n x0 lt0
- f(1) x0 x1 1 x2 12 xn 1n
- x0 x1 x2 xn gt 0
- since f is strictly increasing and continuous,
- root c0 satisfies the 0 lt c0 lt1 and
- IRR r0 (1/ c0) 1 is positive
41
Internal Rate of Return (Contd)
- Remark. One can make up cash flow streams where
no positive real root exists, or even where roots
are complex numbers. To do so you must violate
the hypotheses of the IRR Theorem. These
hypotheses are usually reasonable. - Note. Entries in CFS can be 0.
42
Net Present Value (NPV)
- Definition
- NPV PV of benefits - PV of costs
43
NPV in EXCEL
44
Evaluation Criterion NPV or IRR
- Example. Cutting Trees.
- Units in terms of 100,000.
- a) (-1,2) cut in one year
- b) (-1,0,3) cut after two years
- NPV Approach, assuming r 10
- a) NPV -1/1 2/(1.1) 0.82
- b) NPV -1/1 0/(1.1) 3/(1.1)2 1.48 gt 0.82
- Cut after two years choose option b)
45
Evaluation Criterion NPV or IRR (Contd)
- IRR Approach, c 1/(1r) ? r 1/c - 1
- a) 0 -1 2 c ? c ½ ? r 1, i.e., 100
- b) 0 -1 0 c 3 c2 ? c2 1/3 ? c 1/?3 ?
- r ?3 1 ? 0.732 lt 1.
- Cut after one year choose option a).
46
Evaluation Criterion NPV or IRR (Contd)
- Different decisions depending on evaluation
criterion - NPV gives b), IRR gives a).
- Insight. Use a longer planning horizon, reinvest
all earnings. Which looks better in 6 years? - a) 1 gt 2 gt 4 gt 8 gt 16 gt 32
gt 64 - cash flow stream (-1,0,0,0,0,0,64)
- b) 1 in 2 yearsgt 3 in 2 yearsgt 9
in 2 years gt 27 - cash flow stream (-1,0,0,0,0,0,27)
- a) Business doubles every year.
- b) Business triples every two years ? increases
by ?3 every year (in long run). - Multiplication coefficient is called grows rate
(GR) - since 2 gt ?3, a) has larger grows rate.
47
Evaluation Criterion NPV or IRR (Contd)
- a) IRR 2-1 for cut every year
- b) IRR ?3 1 for cut every 2 years
- This is no accident, but a general result. The
project with largest IRR also has the highest
growth rate.
48
Evaluation Criterion NPV or IRR (Contd)
- Conclusion 1. When the proceeds of the
investment can be repeatedly reinvested in the
same type of project but scaled in size, it makes
sense to choose the project with largest IRR to
get the greatest growth of capital. - Conclusion 2. NPV makes more sense for
one-shot projects.
49
Evaluation Criterion NPV or IRR (Contd)
- If we studied the cutting tree project for a
longer horizon than 1 year, the NPV approach
would also choose a). (Note with a longer
horizon there is ALSO more uncertainty. Further,
these rates of growth cannot continue
indefinitely.) - a) (-1,0,0,0,0,0,64) NPV 35.13
- b) (-1,0,0,0,0,0,27) NPV 14.24
- Theorists agree that, overall, the best criterion
is based on NPV. It provides consistency and
rationality.
50
Other Evaluation Factors
- 1) Which interest rate should we choose for NPV?
- the rate the bank pays on CDs
- the rate paid by the 3-month US Treasury bill
- the rate paid by the highest grade commercial
bond - the cost of capital rate the company must offer
to potential investors in company - 2) PV is not the whole story about the rate of
return. - Alternative 1. Invest 1,000, get a NPV of 100.
- Alternative 2. Invest 1,000,000, get a NPV of
100. - If you had 1,000,000, which alternative would
you choose?
51
Simplico Gold Mine
- You can lease a gold mine from its owners for up
to ten years. The lease is an up-front payment. - You can extract up to 10,000 oz. per year
- Each oz. costs 200.
- Market selling price for gold is 400/oz.
- Interest rate is 10
- All this information remains constant over the
10-year period (heroic assumption).
52
Simplico Gold Mine (Contd)
- Question. What is the most you would be willing
to pay for the lease?
53
Simplico Gold Mine (Contd)
- Answer. Compute PV of income from the mine,
assuming you operate it at full capacity for all
10 years. - Annual profit is (400 - 200) ? 10,000 oz/year
- 2 M.
- PV of annual profit for 10 years
- PV (2 M)/(1.1) (2M)/(1.1)2
(2M)/(1.1)10 12.29 M - If you paid more than 12.29M for the lease, you
would lose money on this undertaking.
54
Warnings
- Cash Flow Warning For each period t,
- cash flow income expense
- i.e., net income. Dont forget the net idea.
- Apples Oranges Warning for Cycle Problems. Be
certain to compare alternatives over the same
time horizon. The horizon can either be finite
or, in some cases, of indefinite length.
55
Automobile Purchase
- Alternative A.
- Car A costs 20,000
- Has annual maintenance cost of 1,000
- Has a useful lifetime of 4 years
- Has no salvage value
- Alternative B.
- Car B costs 30,000
- Has annual maintenance cost of 2,000
- Has a useful lifetime of 6 years
- Has no salvage value
56
Automobile Purchase (Contd)
- These alternatives are NOT over the same time
horizon. We can try a planning horizon of 12
years (3 Car As, 2 Car Bs). - Car A Analysis (3 cycles of 4 years each)
- One Cycle PV
- PVA 20,000 1,0001/(1.1) 1/(1.1)2
1/(1.1)3 - 22,487.
- Three Cycle PV (note the trick used here)
- PVA3 PVA 1 1/(1.1)4 1/(1.1)8 48,336.
57
Automobile Purchase (Contd)
- Car B Analysis (2 cycles of 6 years each)
- One Cycle PV
- PVB 30,000 2,0001/(1.1) 1/(1.1)2
- 1/(1.1)5
- Two Cycle PV (similar trick)
- PVB2 PVB 1 1/(1.1)6 58,795.
- Conclusion. For the 12-year period, using 3 of
Car A is cheaper than using 2 of Car B.
58
Machine Replacement
- How often should we replace a machine? Planning
horizon length is not known in advance - Purchase cost is 10,000 (would need to adjust
for inflation in reality) - First year operating cost is 2,000, no salvage
value. - Machine operating costs increases by 1,000 each
year (these costs incurred at end of year).
59
Machine Replacement (Contd)
- Replacing Machine Every Year
- Machine 1 CFS (-10,-2)
- Machine 2 CFS (0,-10,-2)
- Machine 3 CFS (0,0,-10,-2)
- etc
- Each stream looks identical to the one before,
except it starts one year later (and so must be
discounted by 10). - Conclusion. For an indefinite number of 1-year
replacements, - PV 10 2/(1.1) PV/(1.1) ? PV 130
- (i.e., 130,000)
60
Machine Replacement (Contd)
- Replacing Machine Every 2 Years
- Machine 1 CFS (-10,-2,-3)
- Machine 2 CFS (0,0,-10,-2,-3)
- Machine 3 CFS (0,0,0,0,-10,-2,-3)
- etc
- Each stream looks identical to the one before,
except it starts two years later (and so must be
discounted by 10 for 2 years). - PV 10 2/(1.1) 3/(1.1)2 PV/(1.1)2
- 14.2975 PV/1.21
- 1.21 PV PV 1.21 ? 14.2975 ? PV 82.381
61
Replacing Machine Every k Years
- PV (cost of one cycle of k years) PV/(1.1)k ?
- (1.1)k 1 PV (1.1)k ? cost of 1 cycle of k
years ? - PV (1.1)k ? cost of 1 cycle of k years /
(1.1)k-1 - Just compute the cost of one cycle of k years,
and then compute the PV using the latter formula.
62
Replacing Machine Every k Years
- See Table 2.3, p. 31. Replacing machine every 5
years is cheapest.
63
Taxes
- Suppose you can get 100/year in dividends
annually for two years. You are in the 28
income tax bracket. The time value of money is
10. - Not considering taxes, the PV of dividends is
- PVno tax 100/1.1 100/(1.1)2 90.91
82.64 - 173.55
- Due to taxes, 100 gt (1-0.28)100 72 ,
- the actual PV of the dividends is
- PVtaxes 72/1.1 72/(1.1)2 65.45 59.50
- 124.95.
64
Taxes (Contd)
- Consequently
- PVno tax 100 / 1.1 100 / (1.1)2
- PVtaxes (1-.28)100 / 1.1 (1-.28)100 / (1.1)2
- (1-.28) PVno tax
- To get PV with taxes
- You might now reject a project you would
otherwise accept.
65
Taxes (Contd)
- Assuming this tax rate is applied to all revenues
and expenses (it might not be), IRR would be
identical with or without taxes, e.g., - k 100/(1r) 100/(1r2) ?
- (1-t) k (1-t) 100/(1r) (1-t) 100/(1r2)
66
Taxes (Contd)
- When a uniform tax rate is applied to all
revenues and expenses as taxes and credits
respectively, recommendations from before-tax and
after-tax analyses are identical. - Example. Pay 150, today. Int. rate is 10, tax
rate 28. - Alternative A. Get 100 in 1 year, 100 more in
2 years. - Alternative B. Get 150 in 1 year, 50 more in 2
years.
67
Taxes (Contd)
- Alternative A.
- PVno tax 100/1.1 100/(1.1)2 90.91 82.64
173.55 - PVtaxes 72/1.1 72/(1.1)2 65.45 59.50
124.95. - Alternative B.
- PVno tax 150/1.1 50/(1.1)2 136.36
41.32 177.68 - PVtaxes 108/1.1 36/(1.1)2 98.18 29.75
127.93. - For comparison purposes, with, or without taxes,
Alternative B looks better. However, if you want
to know the actual PV with taxes, then you must
use the tax rate.
68
Depreciation Example
- We buy a machine for 10,000.
- It has a useful life of 4 years.
- It generates a cash flow of 3,000 each year.
- It has a salvage value of 2,000.
- The government requires depreciating the cost of
the machine over its useful life, e.g., if its
net cost to us over 4 years is 10,000 2,000
8,000, with straight-line depreciation we report
its annual cost each year as 8,000/4 2,000 .
69
Depreciation Example (Contd)
- Thus the taxable income it produces each year is
3,000-2,000 1,000. - If the combined federal and state tax rate is
43, we pay 430 tax each year. NPV is computed
at 10.
70
Depreciation Example (Contd)
- Bad News. Without taxes, NPV 876, so this
operation would be profitable. With taxes, NPV
-487, so it would not be.
71
Points About Inflation
- A new Volkswagen bug cost about 2,200 in 1962.
Today it costs about 16,000. - A good starting masters salary in IE was about
10,000 in 1962. What is it today? - Inflation is now running 2 to 3 a year in the
US. Some years it has been as much as 7 to 8
in the US during the last twenty years. - Some other countries have experienced
hyper-inflation. In Germany just after WW I, a
weeks wages could not be carried in both arms.
72
Inflation
- Inflation is an increase in general prices over
time - Inflation rate f prices are multiplied by (1f
) . - Constant (also called real) dollar keeps the
same purchasing power. - Actual (also called nominal, inflated, market )
dollars are used in transactions. - Let r be nominal interest rate, than the real r0
interest rate is given by - 1r0 (1r )/(1f )
- and
- r0 (r - f )/(1f )
73
Inflation (Contd)
- Money in the bank increases (nominally) by 1r ,
- but purchasing power is deflated by 1/(1f)
- Example. Inflation rate f0.04 ,
- nominal rate r 0.1, real rate r0 equals
- r0 (r - f )/(1f )(0.1- 0.04 )/(1
0.04)0.0577
74
Inflation (Contd)
- Question. What happens to the real rate of
interest if the rate of inflation exceeds the
nominal rate of interest? - Warning. Dont mix nominal dollars and real
dollars! Work consistently with one or the
other.
75
Inflation (Contd)
76
Inflation (Contd)
- The real cash flow has all values in todays
dollars. The nominal cash flows has values in
future years adjusted for inflation, e.g., 5000
5200/(1.04), so 5200 in a year is worth 5000
today. 5000 5408/(1.04)2, so 5408 in two years
is worth 5000 today, etc. - We get the same result either way (apart from
rounding errors).
77
Inflation (Contd)
- Note. It is common to estimate cash flow in
constant/real dollars relative to the present,
because then ordinary price increases (ones due
to inflation) can be neglected in a simple
estimation of cash flows. - Effects of Inflation on a 2,000 annual IRA
example is in the file infln-bp.xls