Continuous Probability Distributions
Title:
Continuous Probability Distributions
Description:
... bearings, requires ball bearings 10 1 mm, what percentage of the ball bearings ... that a randomly chosen ball bearing will have a diameter less than 9.75 mm? ... –
Number of Views:78
Avg rating:3.0/5.0
Title: Continuous Probability Distributions
1
Continuous Probability Distributions
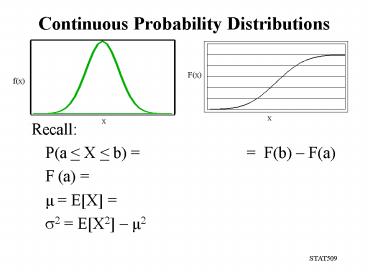
- Recall
- P(a lt X lt b) F(b)
F(a) - F (a)
- µ EX
- s2 EX2 µ2
F(x)
f(x)
x
x
2
Continuous Uniform Distribution
- f(xA,B) 1/(B-A), A lt x lt B
- where A,B is an interval on the real number
line - µ (A B)/2 and s2 (B-A)2/12
1/(B-A)
3
Continuous Uniform Distribution
- EX Let X be the uniform continuous random
variable that denotes the current measured in a
copper wire in milliamperes. 0 lt x lt 50 mA. The
probability density function of X is uniform. - f(x) , 0 lt x lt 50
- What is the probability that a measurement of
current is between 20 and 30 mA? - What is the expected current passing through the
wire? - What is the variance of the current passing
through the wire?
4
Normal Distribution
- n(xµ,s)
- EX µ and VarX s2
f(x)
x
5
Normal Distribution
- Many phenomena in nature, industry and research
follow this bell-shaped distribution. - Physical measurements
- Rainfall studies
- Measurement error
- There are an infinite number of normal
distributions, each with a specified µ and s.
6
Normal Distribution
- Characteristics
- Bell-shaped curve
- -? lt x lt ?
- µ determines distribution location and is the
highest point on curve - Curve is symmetric about µ
- s determines distribution spread
- Curve has its points of inflection at µ s
- µ 1s covers 68 of the distribution
- µ 2s covers 95 of the distribution
- µ 3s covers 99.7 of the distribution
7
Normal Distribution
s
s
s
s
µ
8
Normal Distribution
n(x µ 0, s 1)
n(x µ 5, s 1)
f(x)
x
9
Normal Distribution
n(x µ 0, s 0.5)
f(x)
n(x µ 0, s 1)
x
10
Normal Distribution
n(x µ 5, s .5)
f(x)
n(x µ 0, s 1)
x
11
Normal Distribution
µ 1s covers 68
µ 2s covers 95
µ 3s covers 99.7
12
Standard Normal Distribution
- The distribution of a normal random variable with
mean 0 and variance 1 is called a standard normal
distribution.
13
Standard Normal Distribution
- The letter Z is traditionally used to represent a
standard normal random variable. - z is used to represent a particular value of Z.
- The standard normal distribution has been
tabularized.
14
Standard Normal Distribution
- Given a standard normal distribution, find the
area under the curve - (a) to the left of z -1.85
- (b) to the left of z 2.01
- (c) to the right of z 0.99
- (d) to right of z 1.50
- (e) between z -1.66 and z 0.58
15
Standard Normal Distribution
- Given a standard normal distribution, find the
value of k such that - (a) P(Z lt k) .1271
- (b) P(Z lt k) .9495
- (c) P(Z gt k) .8186
- (d) P(Z gt k) .0073
- (e) P( 0.90 lt Z lt k) .1806
- (f) P( k lt Z lt 1.02) .1464
16
Normal Distribution
- Any normal random variable, X, can be converted
to a standard normal random variable - z (x µx)/sx
17
Normal Distribution
- Given a random Variable X having a normal
distribution with µx 10 and sx 2, find the
probability that X lt 8.
z
x
4
6
8
10
12
14
16
18
Normal Distribution
- EX The engineer responsible for a line that
produces ball bearings knows that the diameter of
the ball bearings follows a normal distribution
with a mean of 10 mm and a standard deviation of
0.5 mm. If an assembly using the ball bearings,
requires ball bearings 10 1 mm, what percentage
of the ball bearings can the engineer expect to
be able to use?
19
Normal Distribution
- EX Same line of ball bearings.
- What is the probability that a randomly chosen
ball bearing will have a diameter less than 9.75
mm? - What percent of ball bearings can be expected to
have a diameter greater than 9.75 mm? - What is the expected diameter for the ball
bearings?
20
Normal Distribution
- EX If a certain light bulb has a life that is
normally distributed with a mean of 1000 hours
and a standard deviation of 50 hours, what
lifetime should be placed in a guarantee so that
we can expect only 5 of the light bulbs to be
subject to claim?
21
Normal Distribution
- EX A filling machine produces 16oz bottles of
Pepsi whose fill are normally distributed with a
standard deviation of 0.25 oz. At what nominal
(mean) fill should the machine be set so that no
more than 5 of the bottles produced have a fill
less than 15.50 oz?
22
Relationship between the Normal and Binomial
Distributions
- The normal distribution is often a good
approximation to a discrete distribution when the
discrete distribution takes on a symmetric bell
shape. - Some distributions converge to the normal as
their parameters approach certain limits. - Theorem 6.2 If X is a binomial random variable
with mean µ np and variance s2 npq, then the
limiting form of the distribution of Z (X
np)/(npq).5 as n ? ?, is the standard normal
distribution, n(z0,1).
23
Relationship between the Normal and Binomial
Distributions
- Consider b(x15,0.4). Bars are calculated from
binomial. Curve is normal approximation to
binomial.
24
Relationship between the Normal and Binomial
Distributions
- Let X be a binomial random variable with n15 and
p0.4. - P(X5) ?
- Using normal approximation to binomial
- n(3.5ltxlt4.5µ6, s1.897) ?
- Note, µ np (15)(0.4) 6
- s (npq).5 ((15)(0.4)(0.6)).5 1.897
25
Relationship between the Normal and Binomial
Distributions
- EX Suppose 45 of all drivers in a certain state
regularly wear seat belts. A random sample of 100
drivers is selected. What is the probability
that at least 65 of the drivers in the sample
regularly wear a seatbelt?