DiversityMultiplexing Tradeoff in Multiple Access Channels

1
Diversity-Multiplexing Tradeoff in Multiple
Access Channels
D. Tse, P. Viswanath, and L. Zheng
EE 360 Paper Presentation Presented by Jeff
Wu April 23, 2004
2
Two Benefits of Multiple Antennas
Diversity Gain Combats fading. Examples include
selection and maximal ratio combining.
Spatial Multiplexing Gain With MIMO systems, can
effectively create several parallel,
non-interfering channels.
n1
x1
y1
?1
nr



xr
yr
?r
Tradeoff characterized by Zhang and Tse for
single user case.
This paper Extension to multiple access channels.
3
(Narrowband) Channel Model
Y (SNR/m)1/2 ?i Hi Xi W

• SNR is high.
• K users, each with m transmit antennas.
• Single receiver with n antennas.
• Codeword Xi is L symbols long, each symbol a
  complex vector of length m.
• Power EXiF2 ? mL.
• W is (n, L) additive noise matrix, iid CN(0,
  1).
• Hi is (n, m) normalized channel matrix for user
  i, entries are iid CN(0, 1) (richly scattered
  Rayleigh fading)

Very important Hi known at the receiver but not
at the transmitter.
4
Definition of Diversity Gain
For high SNR, average probability of error for
BPSK in the single antenna case is (recall way
back in EE359)
Pe ? 1/4 SNR-1
General case Let C(SNR) be a family of codes
indexed by SNR. If
log Pe(SNR)
lim
? -d
log SNR
SNR ? ?
then this family of codes achieves a diversity
gain of d.
Thus the single antenna BPSK case has a diversity
gain of 1.
The higher the diversity gain, the faster Pe
decays as SNR increases.
5
Definition of Multiplexing Gain
With no fading, capacity of a single-user single
antenna AWGN channel is approximately log(SNR),
for high SNR.
General case Let C(SNR) be a family of codes
indexed by SNR. If for each user i,
Ri(SNR)
lim
? ri
log SNR
SNR ? ?
then this family of codes achieves multiplexing
gains of r1, r2, , rK.
The multiplexing gain is the rate increase over
the single antenna AWGN channel capacity.
6
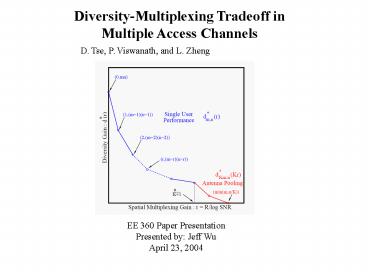
Single User Tradeoff
dm,n(r) Supremum of diversity gains given a
multiplexing gain of at least r. rm,n(d)
Inverse of dm,n(r)
Theorem (Zhang and Tse, 2002) Given that L ? m
n 1,
dm,n(r) (m r)(n r)
for all integer 0 ? r ? min(m, n). Moreover
dm,n(r) is linear between any two integers.
7
Multiple Access Case
Main Theorem The set of all multiplexing gains
given that a diversity gain of at least d (i.e.
error exponent) is described by the following
region
?i?S ri ? rSm,n(d), for all subsets S of
users
Sum of multiplexing gains in S.
Optimal multiplexing gain given a that the users
in S combine into one superuser.
Note the striking similarity to the actual rate
region of a MAC channel!
8
Symmetric Multiplexing Gains
A direct result of the main theorem
Theorem Given that each user has the same
multiplexing gain r, the optimal diversity gain
is given by
dm,n(r), if r ? n/(K1) (Light-loaded
regime) dKm,n(Kr), if r ? n/(K1) (Heavy-loaded
regime)
Note Valid range for r is 0 ? r ? min(m, n/K)
9
Example 1 Adding a Transmit Antenna
Consider when m 1 and n/(K1) gt 2. Here

• Valid range for r is 0 ? r ? m 1 (Limited by
  m).
• System is well within light-loaded regime for
  all r (by more than a factor of 2)

Results from adding tramsmit antenna

• Valid range for r increases to 2.
• System is still within light-loaded regime.
• Allows for both increases in r and in d.

Conclusion Adding a transmit antenna to each
user is very good!
10
Example 2 Adding a Transmit Antenna
Now consider when m 1 and n/K ? 1

• Valid range for r is 0 ? r ? n/K (Limited by n).
• Both light-loaded and heavy-loaded regimes exist.

Results from adding transmit antenna

• Range for r does not increase.
• Good performance improvement in light-loaded
  region, but not as dramatic in more heavy
  loaded-region.

11
Example 3 Adding a Receive Antenna and a User
Consider when m 1 and n/(K1) 1

• Valid range for r is 0 ? r ? m 1 (Limited by
  m).
• Light loaded region is also 0 ? r ? n/(K1) 1

Suppose we add both a receive antenna and a user.
n1

• Valid range for remains same.
• Light loaded region also same.
• Performance still increases!

n
Somewhat surprising result With an extra
antenna, we can add an extra user and still
experience increased performance across the board.
n-K1
Optimal diversity gain, d(r)
0
1
Multiplexing gain, r
12
Caveats
We assume that receiver is optimum ML receiver.

• Authors show that for V-BLAST systems, adding
  one user and one reciever will make the
  diversity-multiplexing tradeoff unchanged.
• Authors show that other suboptimal methods (such
  as successive cancellation) do not sufficiently
  close this performance gap.

13
Error Events
The sharp difference between the light-loaded and
the heavy-loaded regimes manifest themselves in
the error events. Authors show that

• For the light-loaded regime, an error is almost
  always due to a single users codeword being
  decoded incorrectly.
• For the heavy-loaded regime, an error is almost
  always due to all the users codewords being
  decoded incorrectly.

Possible implications for designing retransmit
protocols
14
Conclusions

• Fundamental tradeoff between diversity and
  spatial multiplexing.
• Single user case Tradeoff is piecewise linear
  function.
• Symmetric multiple access case Tradeoff is
  piecewise linear, with possibly two different
  regimes A light-loaded and a heavy-loaded
  regime.
• Tradeoff shows that substantial gains can be
  achieved by multiple antennas in the MAC channel.
• Still a substantial gap between optimal results
  and suboptimal methods used today.