Decision Tree Classifier - PowerPoint PPT Presentation
1 / 38
Title:
Decision Tree Classifier
Description:
If trainset is purely class c: Create a leaf node that predicts c. Otherwise: ... Content in a DNA Binding Site. Encoding. Class Distribution. Entropy ... – PowerPoint PPT presentation
Number of Views:145
Avg rating:3.0/5.0
Title: Decision Tree Classifier
1
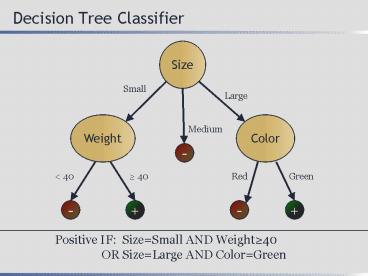
Decision Tree Classifier
Positive IF SizeSmall AND Weight40
OR SizeLarge AND ColorGreen
2
Feature Space
Feature 2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Feature 1
3
Feature Space
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Feature 2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Feature 1
4
How Decision Trees Divide Feature Space?
-
-
-
-
-
-
-
-
Feature 2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Feature 1
5
How Decision Trees Divide Feature Space?
- -- -
- - - - -
Nominal Feature
- - - -------- -- --- - -
Continuous Feature
6
Feature Space
-
-
Feature 2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Feature 1
7
Growing a Tree Top-Down
50,50-
-
8
Growing a Tree (Based on ID3, Quinlan 1986)
- Function grow(trainset)
- If trainset is purely class c
- Create a leaf node that predicts c.
- Otherwise
- Create an interior node
- Choose an split feature f
- For each value v of feature f
- subtree grow(subset of trainset with fv)
- return new node
9
Toy Data Set
10
Decision Tree For Toy Data Set
11
Decision Tree For Toy Data Set
Shape
Triangle
Circle
Square
-
-
12
Splitting Choices
50 50-
50 50-
13
Splitting Choices
50 50-
14
Splitting Choices
50 50-
15
Entropy
- Entropy measures the amount of information
contained in a message - Measured in bits
16
Entropy
- An event with two equally-probable outcomes has
an entropy of 1 bit - An event with two outcomes that are not equally
probable has an entropy lt 1 bit - An event with two outcomes, A and B, such that
P(A)1 and P(B)0 has zero entropy
17
Information Content in a DNA Binding Site
18
A 4-Class Classification Problem (Case 1)
19
A 4-Class Classification Problem (Case 2)
20
Information Gain
50 50-
Entropy 1.0
51 examples, Entropy 0.918
19 examples, Entropy 0.297
30 examples, Entropy 1.0
21
Information Gain
50 50-
Entropy 1.0
19 examples, Entropy 0.485
60 examples, Entropy 0.997
21 examples, Entropy 0.276
22
Handling Continuous Features
Training Data
Class Age
Info_Gain 0.125
Age
23
Tree Sizes on Adult Data Set
24
Test Set Accuracy on Adult Data Set
Random splitting has a standard deviation of
about 0.5 percentage points
25
Summary
- We search the space of possible trees
- Our search bias Preference for smaller trees
- Deliberate decison
- Occams razor principle
- Our heuristic metric Information Gain
- Based on entropy calculation
- Basis for ID3 Algorithm (Quinlan, 1986)
26
Learning and Growing
27
Exclusive OR
28
Growing but not Learning
29
XOR Feature Space
-
x1
-
x2
30
Toy Data Set
31
Decision Tree For Toy Data Set
Example ID
1
2
5
4
3
-
-
-
32
Gain Ratio
33
Test Set Accuracy, Adult Data Set
34
Accuracy and Tree Size (Adult Data Set)
35
Pruning Algorithm
- Compute tuning set accuracy
- For each interior node
- Consider pruning at that point (i.e. make it a
leaf with the majority training set
classification among examples compatible with the
path) - Recompute tuning set accuracy
- If no such pruning step improves tuning set
accuracy, quit - Otherwise, prune the node that results in the
highest accuracy, and repeat
36
Accuracy and Tree Size, Adult Data Set
37
Test Set Accuracy on Adult Data Set
Random splitting has a standard deviation of
about 0.5 percentage points
38
Big Fat Summary
- Decision trees have a low-bias hypothesis space
- Can represent concepts that higher-bias
classifiers (e.g. Naïve Bayes) cannot - Higher hypothesis variance can overfit
- Decision trees are human-readable
- Learn trees using Info_Gain heuristic
- Prune trees using greedy approach