Lever Rule

1
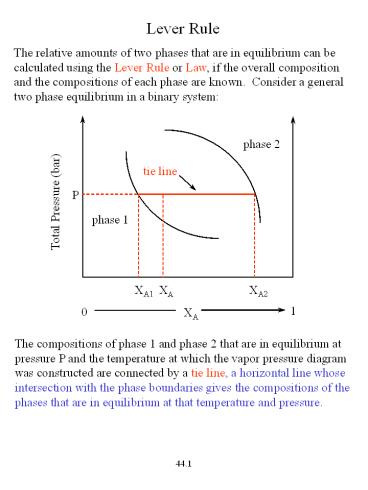
Lever Rule The relative amounts of two phases
that are in equilibrium can be calculated using
the Lever Rule or Law, if the overall composition
and the compositions of each phase are known.
Consider a general two phase equilibrium in a
binary system
The compositions of phase 1 and phase 2 that are
in equilibrium at pressure P and the temperature
at which the vapor pressure diagram was
constructed are connected by a tie line, a
horizontal line whose intersection with the phase
boundaries gives the compositions of the phases
that are in equilibrium at that temperature and
pressure.
2
For ntotal moles distributed at equilibrium
between phases 1 and 2 we can we can calculate
the number of moles of component A as nA XA
ntotal XA (n1 n2) XA n1 XA n2 We
can also calculate the moles of component A
by nA nA1 nA2 XA1 n1 XA2
n2 Equating these two expressions for nA
gives XA n1 XA n2 XA1 n1 XA2
n2 which can be rearranged to give the lever
law n1 (XA - XA1) n2 (XA2 - XA) Can you
see why this expression is called the lever law
(hint - think of the tie line as a teeter
totter)? The lever law can also be expressed in
terms of masses and a weight percent or weight
fraction axis. Write the lever law in terms of
masses and weight fractions.
3
While the above form of the lever law best
illustrates its name, it is not the most
convenient expression of the law. We will derive
a more convenient form using a binary boiling
point diagram with a weight axis
We start with the lever law that we just
derived m1 (wA - wA1) m2 (wA2 - wA) and
solve for the ratio of the masses in the two
phases (wA2 - wA) / (wA - wA1) m1 / m2
m1 / (mtotal - m1) This expression can be
arranged to give a form of the lever law which
gives the ratio of the mass in phase 1 to the
total mass m1 / mtotal (wA2 - wA) / (wA2
- wA1) How are the terms on the right side of
this expression related to the tie line?
4
Can you write down the expression that would give
the fraction of the mass present in phase 2? Can
you write down the expressions for the ratio of
the moles in phase 1 and 2 to the total moles?
5
Suppose the pressure is reduced over 100.0 grams
of toluene and benzene, which is 25.0 weight in
toluene. What masses of toluene and benzene are
present in the liquid and vapor phases when the
pressure has been reduced to a point where the
weight fraction of toluene in the vapor phase is
0.170 and the weight fraction of toluene in the
liquid phase is 0.400?
liquid
Total Pressure (bar)
vapor
0.250
0.170
0.400
100
0
wT
What is the total mass in the vapor phase? What
is the total mass in the liquid phase? What are
the masses of toluene and benzene in the vapor
phase? What are the masses of toluene and benzene
in the liquid phase?
6
A constant temperature tie line on a binary phase
diagram intersects a liquid phase that is 33.9
mole alcohol and a liquid phase that is 80.5
mole alcohol. If a mixture of 4.00 moles of
ethanol and 2.00 moles of water are brought to
equilibrium at this temperature, calculate the
moles of ethanol and water in each of these
phases.