Size of the Remaining Graph

1
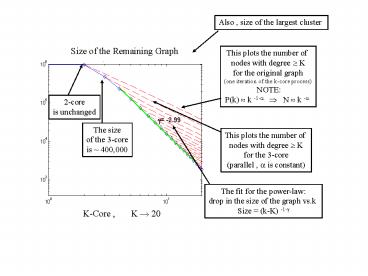
Also , size of the largest cluster
Size of the Remaining Graph
This plots the number of nodes with degree ?
Kfor the original graph (one iteration of the
k-core process) NOTE P(k) ? k -1-? ? N ? k
-?
2-coreis unchanged
The sizeof the 3-coreis 400,000
This plots the number of nodes with degree ?
Kfor the 3-core (parallel , ? is constant)
The fit for the power-lawdrop in the size of
the graph vs.k Size (k-K) -1-?
K-Core , K ? 20
2
Size of the Remaining Graph , (referenced to
degree distribution)
Parameters M 1 , L 1,2,4,8 over 106
nodes Model In case of parallel links count
links (and not of neighbors) Deg. Distribution
the power,? (as in P(k) ? k -1-? ), goes from
1.4 to 1.8
Notes - Before KL , K-core does not change
the graph (trivial) - Above, the size of the
graph drops with a power of (1 L/M) - The
dashed (red) line is the size of the graph after
dropping all nodes with an initial
degree of lt K , (a transformed deg. dist plot)
3
Size of the Remaining Graph , (referenced to the
degree distribution)
Parameters L 1 , M 1,2,4,8 over 106
nodes Model In case of parallel links count
links (and not of neighbors) Deg. Distribution
the power,? (as in P(k) ? k -1-? ), goes from
1.4 to 1
Notes - The size of the graph drops with a
power of (1 L/M) - As M is greater, the
plot of graph size converges to the dashed line.
(the distance between the lines is the
number of nodes that initially had deg. ? K ,
but were dropped out at a later stage)
4
The Strongly Connected Fraction of the Graph
This is the (extrapolated) point,core at which
the graph is entirely strongly connected
This point (for example)means that for the
10-core, 8 of the graph is strongly connected
Log(K) , as in k-core
In this example , the graph is unchanged under
2-core.
Definition A cluster is said to be strongly
connected if there is a path (directed) between
any two nodes in it.
Log (fraction)
5
The Strongly Connected Fraction of the Graph
Parameters M 1 , L 1,2,4,8 over 106
nodes Model In case of parallel links count
neighbors (and not of links)
Plotting the core at which the graphis strongly
connected(extrapolating)for L1 , -- 53th
core L2 , -- 33th core L4 , -- 26th
core L8 , -- 20th core
Log Core
L1 L2 L4 L8
6
The Strongly Connected Fraction of the Graph
Parameters L 1 , M 1,2,4,8 over 106
nodes Model In case of parallel links count
neighbors (and not of links)
Plotting the core at which the graphis strongly
connected(extrapolating)for M1 , -- 53th
core M2 , -- 112th core M4 , -- 512th
core M8 , --2240th core
Log Core
M1 M2 M4 M8