Biermann Battery

1
The Biermann Battery and First Structure
Formation Fen Zhao Advisor Tom
Abel Collaborators Marcelo Alvarez, Matthew Turk
Abstract It is still unclear what the magnitude
and effects of magnetic fields are in the early
universe. Using the ENZO, a 3D adaptive mesh
cosmological simulation code, we look at the
statistics of magnetic fields generated in early
structure formation by the Biermann battery
process. Tracking six species (H, H, He, He,
He and e-), we follow the formation of
structure from multiple independent realizations
of cosmological initial conditions to better
understand how magnetic fields are generated by
non aligned pressure and density gradients. These
efforts are part of the larger framework of
adding ideal MHD to the ENZO software.

• Biermann Battery
• As a result of including a electron pressure
  gradient term in the generalized Ohms Law, a
  term (the Biermann battery) (1) appears in the
  fluid equations which generates a magnetic field.
• Here ne and pe are the electron number density
  and pressure. Currently we can measure ambient
  galactic magnetic fields of a few microGauss with
  Faraday rotation measurements. The Biermann
  battery is one candidate for the source of a seed
  magnetic field (to be amplified via the
  traditional alpha-omega dynamo) that can generate
  the magnetic fields we see today. Such
  cosmological magnetic fields can affect a variety
  of astrophysical mechanisms such as synchotron
  radiation and angular momentum transfer in star
  formation.
• Preliminary Results
• We use ENZO to follow the evolution of three
  independent cosmological Gaussian initial
  conditions. For each set of cosmological initial
  conditions, we follow with adaptive mesh
  simulations focusing on the five heaviest halos
  that form. Our simulation box is 500 kpc/h, with
  two nested grids, initialized at z99 from an
  Eisenstein and Hsu type power spectrum. We use a
  top grid resolution of 1283 and an effective dark
  matter resolution of 5123. We follow the
  evolution up to z17.We follow the collapse up to
  11 levels of refinement, doubling the resolution
  at each level based on over density in baryon and
  dark matter mass, and resolving the Jeans length.
  This resolves the simulation to 21 pc.
• We approximate the amount of magnetic field
  generated by multiplying the magnitude of the
  Biermann term by the dynamical time
• This gives us an over-estimate but should be in
  the right order of magnitude. We find that 10-22
  Gauss fields are generated. In Siegel and Fry
  (2006), cosmological perturbations at
  recombination are presented as a mechanism for
  generating seed fields of magnitude 10-28 at
  z18. This mechanism would strongly overpower
  that seed field, even at early times.
• Given the magnetic energy density, we can
  calculate the magnetic energy per particle, and
  therefore a temperature. We find that the
  magnetic temperature is 10-31 eV, significantly
  less than the fluid temperature of 0.1eV.
  Therefore the magnetic field should play no role
  in the fluid dynamics of the simulation up to
  redshift z18.

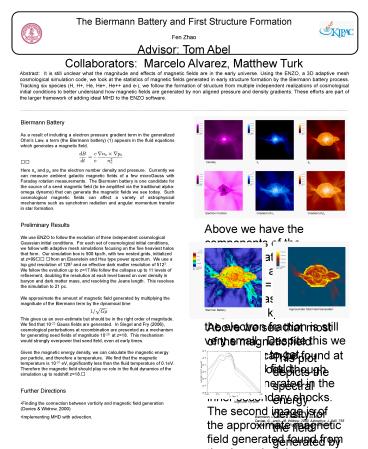
Density
ne
pe
Electron Fraction
Gradient of ne
Gradient of pe
Above we have the components of the Biermann
battery along with density and electron fraction
at z18 for a 2.7 x 106 solar mass halo. Side
length is 40 kpc. Note that the electron
fraction is still very small. Despite this we
are still able to get significant B field
generation.

Approximate Total Field Generated
Bierman Battery
Above we see that most of the magnetic field
generated can be found at the virial shock,
though some is generated in the inner secondary
shocks. The second image is of the approximate
magnetic field generated found from the dynamical
time.
This plot depicts the spectral energy density for
the field generated by cosmological perturbations
at recombination. Even at the peak length
scales, the field is six orders of magnitude
smaller. At the length scales of our simulation,
the field generated is nine orders of magnitude
smaller.
Siegel and Fry 2006
Biermann, L., 1950, Z. Naturforsch. 5A, 65.
Davies, G., and L. M. Widrow, 2000, Astrophys.
J. 540, 755 Siegel, E. R. and J. N. Fry,
arXivastro-ph/0604526