Boolean Algebra

1
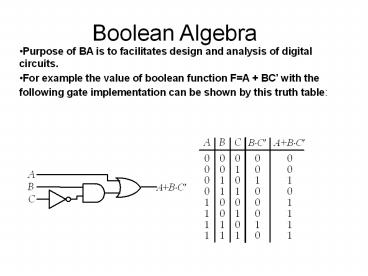
Boolean Algebra

• Purpose of BA is to facilitates design and
  analysis of digital circuits.
• For example the value of boolean function FA
  BC with the following gate implementation can be
  shown by this truth table

2
Boolean Algebra

• Basic identities of boolean algebra

1. X 0 X 3. X 1 1 5. X X X
7. X X 1excluded middle 9. (X ) X
involution 10. X Y Y X 12. X(YZ ) (XY
)Z 14. X(YZ ) XY XZ 16. (X Y )? X ?Y
? 18. X XY X
2. X1 X identity 4. X0 0
base 6. XX X idempotence 8. XX 0
non contradiction 11. XY YX
commutative 13. X(YZ ) (XY )Z
associative 15. X(YZ ) (XY )(XZ )
distributive 17. (XY) X?Y ? demorgan 19.
X.(XY) x absorbtion
3
Basic identities of B.A. can be proven by truth
table
demorgan
distributive
4
Boolean Algebra

• For each algebraic expression the dual of of
  algebraic expression achieved by interchanging
  AND and OR operators and replacing 0s and 1s.
• Parallel columns illustrate duality principle.
  The duality principle states that if E1 and E2
  are Boolean expressions then
• E1 E2 ? dual (E1)dual (E2)
• where dual(E) is the dual of E
• Note 15-17 have no counterpart in ordinary
  algebra.
• Other handy identity.
• XXYXY (15, 7 and 2)

5
Boolean Algebra

• By using boolean algebra rules, a simpler
  expression may be obtained
• Operator Precedence when evaluating boolean
  expression , order of precedence is
• Parentheses
• NOT
• AND
• OR
• For example Look at DeMorgan truth table first
  (xY) is computed then complement of (XY).
• But for x.y first the complement of x and
  complement of y is computed and then the result
  is ANDed

6
Boolean Function Simplification
7
Boolean function simplification

• It means by manipulation of B.A. reducing the
  number of terms and literals in the function. For
  example
• f xyz xyz xy
• x(yz yz) xy
• x (z(yy)) xy
• x(z.1) xy
• xz xy

8
The Consensus Theorem

• Theorem. XY YZ X ?Z XY X ?Z
• Proof. XY YZ X ?Z XY (X X ?)YZ X ?Z
  2,7
• XY XYZ X ?YZ X ?Z 14
• XY(1 Z ) X ?Z(Y 1) 2,11,14
• XY X ?Z
  3,2
• Dual. (X Y )(Y Z )(X ? Z ) (X Y )(X ?
  Z )

9
Complement of a Function

• There are two ways for doing that
• Using DeMorgans theorem
• Taking the dual of the function and complement
  each literal
• For example complements of
• xyz xyz (xy z)(x yz)
• x(yz yz) x (yz)(y z)

10
Canonical and standard Forms

• The sum of products is one of two standard forms
  for Boolean expressions.
• ?sum-of-products-expression? ?p-term?
  ?p-term? ... ?p-term?
• ?p-term? ?literal? ?literal?
  ?literal?
• example. X ?Y ?Z X ?Z XY XYZ
• A minterm is a term that contains every variable,
  in either complemented or un-complemented form.
• example. in expression above, X ?Y ?Z is minterm,
  but X ?Z is not
• A sum of minterms expression is a sum of products
  expression in which every term is a minterm.
• example X ?Y ?Z X ?YZ XYZ ? XYZ is sum of
  minterms expression that is equivalent to
  expression above.
• shorthand list minterms numerically, so X ?Y ?Z
  X ?YZ XYZ ? XYZ becomes 001011110111 or
  Sm (1,3,6,7)

11
Canonical and standard Forms

• The product of sums is the second standard form
  for Boolean expressions.
• ?product-of-sums-expression? ?s-term?
  ?s-term? ... ?s-term?
• ?s-term? ?literal? ?literal?
  ?literal?
• example. (X ?Y ?Z )(X ?Z )(X Y )(X Y Z )
• A maxterm is a sum term that contains every
  variable, in complemented or uncomplemented form.
• example. in exp. above, X ?Y ?Z is a maxterm,
  but X ?Z is not
• A product of maxterms expression is a product of
  sums expression in which every term is a maxterm.
• example. (X ?Y ?Z )(X ?YZ )(XYZ ?)(XYZ )
  is product of maxterms expression that is
  equivalent to expression above.
• shorthand list maxterms numerically so, (X ?Y
  ?Z )(X ?YZ) (XYZ ?)(XYZ ) becomes
  110100001000 or
• P M(6,4,1,0)

12
How to build the boolean function from truth table

• One way is to find a minterms or standard
  products by ANDing the terms of the n variable,
  each being primed if it is 0 and unprimed if it
  is 1. A boolean function can be formed by forming
  a minterm for each combination of variables that
  produce 1 in the function and then taking OR of
  all those forms.
• Another way is by finding maxterms or standard
  sums by OR term of the n variables, with each
  variable being unprimed if corresponding bit is 0
  and primed if it is 1. A boolean function can be
  formed as a product of maxterms for each
  combination of variables that produce 0 in the
  function and then form And of all those forms

13

• For example
• x y z function f1 function f2
  minterms maxterms
• 0 0 0 0
  0 m0 M0
• 0 0 1 1
  0 m1 M1
• 0 1 0 0
  0 m2 M2
• 0 1 1 0
  1 m3 M3
• 1 0 0 1
  0 m4 M4
• 1 0 1 0
  1 m5 M5
• 1 1 0 0
  1 m6 M6
• 1 1 1 1
  1 m7 M7
• Sum of minterms
• f1 xyz xyz xyz m1 m4 m7
• f2 xyz xyz xyz xyx m3 m5 m6
  m7
• Product of maxterms
• f1 (xy z)(xyz)(x y z)(x y z)
  M0M2M3M5M6
• f2 (xyz)(xyz)(xyz)(xyz) M0M1M2M4
  

14
Conversion between Canonical Forms

• By reading from a truth table the two canonical
  forms ( sum of minterms and product of maxterms)
  can be obtained.
• A boolean function can be converted to the
  canonical form. For example
• F xy xy (in form of sum of the products
  S.O.P)
• (z z)xy xz(yy) xyz xyz xzy
  xzy
• can be converted to sum of minterms
• that can be shown by m1m3m6m7 or ?(1,3,6,7)

15
Conversion between Canonical Forms

• To convert it to the product of maxterms
• F xy xy (xy x)(xy z)
• (x x) (x y)(xz)(yz) (xy)(xz)(yz)
• it is in the form of products of sums (P.O.S)
  but we want the product of maxterms. So
• (xy(z.z)) (x z (y.y))(y z (x.x))
• (x y z)(x z y)(x z y)(x y z)
• M0M2M4M5?(0,2,4,5)

16
Conversion between Canonical Forms

• To convert from one canonical form to another,
  interchange the symbol ? and ? and list those
  numbers missing from the total number of minterms
  or maxterms which is 2n,where n is number of
  variables.
• To verify that we convert sum of minterms to the
  product of maxterms by finding the complement of
  a function presented as sum of minterms. From
  the result the product of maxterms can be easily
  obtained
• For example F(x,y,z) m1m3m6m7
  ?(1,3,6,7) the complement of F (presented in the
  form of sum of the minterms) are the minterms
  that makes F to be zero thus
• F(x,y,z) (?(1,3,6,7)) (m0 m2 m4
  m5)
• F (F(x,y,z)) (m0 m2 m4 m5)
• Using Demorgans m0m2m4m5
• since each mj Mj it is M0M2M4M5 ?(0,2,4,5)

17
Standard forms

• Sometimes boolean functions are shown as standard
  forms. For example
• F1 y xy xyz ( sum of products)
• F2 x(y z) (x y z) (product of sums)
• the product and sum can be used to make the
  gate structure consist of AND and OR gates
• Sometimes boolean function can be shown in non
  standard forms
• F3 AB C(D E) can be changed to AB CD CE
• Different forms results different level of
  implementation of logical gates (see the next
  slide)

18
(No Transcript)
19
(No Transcript)
20
(No Transcript)
21
(No Transcript)
22
(No Transcript)
23
(No Transcript)
24
(No Transcript)
25
(No Transcript)