Mining data streams using clustering

1
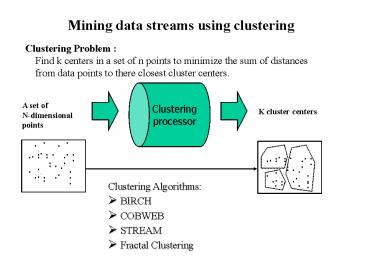
Mining data streams using clustering
Clustering Problem Find k centers in a set
of n points to minimize the sum of distances
from data points to there closest cluster centers.
Clustering processor
A set of N-dimensional points
K cluster centers
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

• Clustering Algorithms
• BIRCH
• COBWEB
• STREAM
• Fractal Clustering

2
K-median algorithm

• Problem Definition
• Given D a set of n points in a metric space,
  choose k medians
• so as to minimize the assignment cost
• the sum of (squared) distances from points to
  nearest centers.
• Given m data points. Find k clusters of these
  points such that the sum
• of the 1-norm distances from each point to the
  closest cluster center is
• minimized.

Two-step algorithm STEP 1 For each set of M
records, Si, find O(k) centers in S1, , Sl
Local clustering Assign each point in Sito its
closest center STEP 2 Let S be centers for S1,
, Sl with each center weighted by number of
points assigned to it. Cluster S to find k
centers
3
Decision trees

• One of the most effective and widely-used
  classification methods
• Induce models in the form of decision trees
• Each node contains a test on the attribute
• Each branch from a node corresponds to a possible
  outcome of the test
• Each leaf contains a class prediction
• A decision tree is learned by recursively
  replacing leaves by test nodes, starting at the
  root

4
Hoeffding trees

• A classification problem is defined as
• N is a set of training examples of the form (x,
  y)
• x is a vector of d attributes
• y is a discrete class label
• Goal To produce from the examples a model yf(x)
  that predict the classes y for future examples x
  with high accuracy

• Hoeffding Bound
• Consider a random variable a whose range is R
• Suppose we have n observations of a
• Mean
• Hoeffding bound states
• With probability 1- ?, the true mean of a is at
  least
• , where

5
VFDT(Very Fast Decision Tree)

• A decision-tree learning system based on the
  Hoeffding tree algorithm
• Split on the current best attribute, if the
  difference is less than a user-specified
  threshold
• Wasteful to decide between identical attributes
• Compute G and check for split periodically
• Memory management
• Memory dominated by sufficient statistics
• Deactivate or drop less promising leaves when
  needed
• Bootstrap with traditional learner
• Rescan old data when time available
• Scales better than pure memory-based or pure
  disk-based learners

6
CVFDT (Concept-adapting VFDT)

• Extension of VFDT
• Same speed and accuracy as VFDT
• Source producing examples may significantly
  change behavior.
• In some nodes of the tree, the current splitting
  attribute may not be the best anymore
• Expand alternate trees. Keep previous one, since
  at the beginning the alternate tree is small and
  will probably give worse results
• Periodically use a bunch of samples to evaluate
  qualities of trees.
• When alternate tree becomes better than the old
  one, remove the old one.
• CVFDT also has smaller memory requirements than
  VFDT over sliding window samples.

7
Experiment resultsVFDT Vs CVFDT

• CVFDT not use too much RAM
• D50, CVFDT never uses more than 70MB
• Use as little as half the RAM of VFDT
• VFDT often had twice as many leaves as the number
  of nodes in CVFDTs HT and alternate sub trees
  combined
• Reason VFDT considers many more outdated
  examples and is forced to grow larger trees to
  make up for its earlier wrong decisions due to
  concept drift

8
Association Rules

• Finding frequent patterns, associations,
  correlations, or causal structures among sets of
  items or objects in transaction databases,
  relational databases, and other information
  repositories.
• Lossy Algorithm
• Sticky algorithm
• Features of the algorithms
• Sampling techniques are used
• Frequency counts found are approximate but error
  is guaranteed not to exceed a user-specified
  tolerance level
• For Lossy Counting, all frequent items are
  reported
• Sticky Sampling is non-deterministic, while Lossy
  Counting is deterministic
• Experimental result shows that Lossy Counting
  requires fewer entries than Sticky Sampling