Gamblers Ruin Problem
1 / 12
Title: Gamblers Ruin Problem
1
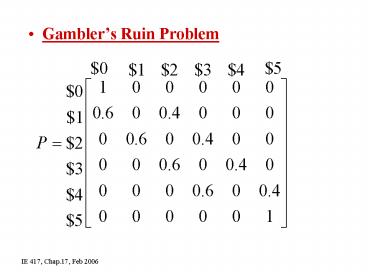
- Gamblers Ruin Problem
IE 417, Chap.17, Feb 2006
2
Chap. 19 Definitions Xt a character of system
at time t unknown before time t, as random
variable Discrete-time stochastic process is a
description of the relation between X0, X1, X2,
..... Markov chain is a special type of
discrete-time stochastic process that state of
system at each time t1 depends only to the
state of system at time before it. pij
transition probability qi prob. to be in
state i at time 0
IE 417, Chap.17, March 00
3
Chap. 19 Definitions A state i is an
absorbing state if pii 1. A state i is a
transient state if there exists a state j that
is reachable from i, but the state i is not
reachable from state j.
IE 417, Chap 17, Jan 99
4
Ergodic Chain ? steady-state distribution ?
? .P replace one equation by ?s ?i
1 mij mean first
passage time mij 1 ?k?j pik mkj mii 1 /
?i
IE 417, Chap 17, Jan 99
5
Computer CenterSource Anderson, Sweeney, and
Williams, An Introduction to Management
ScienceWith added questions.
Transition matrices for 1-hour periods P1is
current situation, P2 is improved situation
IE 417, Chap.17, Feb 2006
6
Computer Center (continued)
- The device that improves the computer centers
performance costs 40,000 and will last for 400
hours. Estimated cost of lost business for each
hour that the center is down is 500. - Would you buy this device?
- Mean first passage time matrix is as below
IE 417, Chap.17, Feb 2006
7
Absorbing Chain transient absorbing
ti aj ti Q
R P aj O
I ti (I - Q)-1 ti
?no of times? aJ (I - Q)-1 R ti
?probability ?
IE 417, Chap 17, Jan 99
8
- Gamblers Ruin Problem (continued)
IE 417, Chap.17, Feb 2006
9
KLM Christmas Tree Farm Source Anderson,
Sweeney, and Williams, An Introduction to
Management Science With added questions 5000
trees 1500 small and 3500 available Will not
plant new trees. Definition of States C Cut
and sold L Lost to disease S Too small for
cutting A Available but not cut and
sold Questions How many of trees will be sold
eventually ? How much are you willing to pay to
buy this farm? What is the expected life of this
business? What is the cash flow diagram for
future income?
IE 417, Chap 19, Feb 2006
10
KLM Trees Transition Matrix (given) C A S L C
1 0 0 0 A .4 .5 0 .1 S .1 .2 .5 .2 L 0 0
0 1
IE 417, Chap 17, Jan 99
11
- KLM Trees (continued)
- Rearranged transition matrix and final
calculations
IE 417, Chap.17, Feb 2006
12
Work Force Planning Hi number hired for group i
at the beginning of each period Ni
number in group i at steady state (census) Pij
probability of those in group i to be in group j
in the next period Hi ?k?I Nk Pki
Ni (1-Pii) for i 1,2,3..,s 1 2 s s
1 1 2 3 . . .
S
IE 417, Chap 17, Jan 99