Hypothesis Testing

1
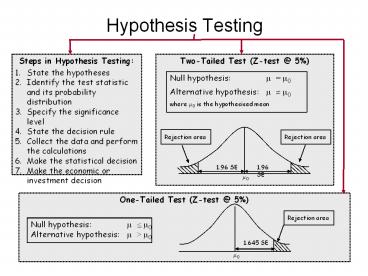
Hypothesis Testing
Steps in Hypothesis Testing 1. State the
hypotheses 2. Identify the test statistic and its
probability distribution 3. Specify the
significance level 4. State the decision
rule 5. Collect the data and perform the
calculations 6. Make the statistical
decision 7. Make the economic or investment
decision
Two-Tailed Test (Z-test _at_ 5)
Null hypothesis ? ?0 Alternative
hypothesis ? ? ?0 where ?0 is the hypothesised
mean
Rejection area
Rejection area
One-Tailed Test (Z-test _at_ 5)
Rejection area
Null hypothesis ? ? ?0 Alternative
hypothesis ? gt ?0
1.645 SE
?0
2
Hypothesis Testing Test Statistic Errors
Test Statistic

• Test Concerning a Single Mean

• Type I and Type II Errors
• Type I error is rejecting the null when it is
  true. Probability significance level.
• Type II error is failing to reject the null when
  it is false.
• The power of a test is the probability of
  correctly rejecting the null (i.e. rejecting the
  null when it is false)

3
Hypothesis about Two Population Means
Normally distributed populations and independent
samples Examples of hypotheses
Population variances unknown and cannot be
assumed equal

• Population variances unknown but assumed to be
  equal
• s2 is a pooled estimator of the common variance
• Degrees of freedom (n1 n2 - 2)

4
Hypothesis about Two Population Means
Normally distributed populations and samples that
are not independent - Paired comparisons
test Possible hypotheses

• Application
• The data is arranged in paired observations
• Paired observations are observations that are
  dependent because they have something in common
• E.g. dividend payout of companies before and
  after a change in tax law

• Symbols and other formula

5
Hypothesis about a Single Population Variance
Possible hypotheses Assuming normal
population

Symbols s2 variance of the sample data ?02
hypothesized value of the population variance n
sample size Degrees of freedom n 1 NB
For one-tailed test use ? or (1 ?) depending on
whether it is a right-tail or left-tail test.
Chi-square distribution is asymmetrical and
bounded below by 0
Obtained from the Chi-square tables. (df, 1 - ?/2
)
Obtained from the Chi-square tables. (df, ?/2)
Higher critical value
Lower critical value
Fail to reject H0
Reject H0
Reject H0
6
Hypothesis about Variances of Two Populations
Possible hypotheses Assuming normal
populations
The convention is to always put the larger
variance on top

Degrees of freedom numerator n1 -
1, denominator n2 - 1
F Distributions are asymmetrical and bounded
below by 0
Obtained from the F-distribution table for ? -
one tailed test ?/2 - two tailed test
Critical value
Fail to reject H0
Reject H0
7
Correlation Analysis
Sample Covariance and Correlation
Coefficient Correlation coefficient measures
the direction and extent of linear association
between two variables
Scatter Plots
x
Testing the Significance of the Correlation
Coefficient Set Ho ?
0, and Ha ? ? 0 Reject null if test
statistic gt critical t
Degrees of freedom (n - 2)
8
Parametric and nonparametric tests

• Parametric tests
• rely on assumptions regarding the distribution of
  the population, and
• are specific to population parameters.
• All tests covered on the previous slides are
  examples of parametric tests.

• Nonparametric tests
• either do not consider a particular population
  parameter, or
• make few assumptions about the population that is
  sampled.
• Used primarily in three situations
• when the data do not meet distributional
  assumptions
• when the data are given in ranks
• when the hypothesis being addressed does not
  concern a parameter (e.g. is a sample random or
  not?)

9
Linear Regression
Basic idea a linear relationship between two
variables, X and Y. Note that the standard error
of estimate (SEE) is in the same units as Y and
hence should be viewed relative to Y.
Mean of ?i values 0
Least squares regression finds the straight line
that minimises
10
The Components of Total Variation
11
ANOVA, Standard Error of Estimate R2
Standard Error of Estimate
Coefficient of determination R2 is the proportion
of the total variation in y that is explained by
the variation in x

• Interpretation
• When correlation is strong (weak, i.e. near to
  zero)
• R2 is high (low)
• Standard error of the estimate is low (high)

12
Assumptions Limitations of Regression Analysis

• Assumptions
• The relationship between the dependent variable,
  Y, and the independent variable, X, is linear
• The independent variable, X, is not random
• The expected value of the error term is 0
• The variance of the error term is the same for
  all observations (homoskedasticity)
• The error term is uncorrelated across
  observations (i.e. no autocorrelation)
• The error term is normally distributed

• Limitations
• Regression relations change over time
  (non-stationarity)
• If assumptions are not valid, the interpretation
  and tests of hypothesis are not valid
• When any of the assumptions underlying linear
  regression are violated, we cannot rely on the
  parameter estimates, test statistics, or point
  and interval forecasts from the regression