Vibrational (Infrared) Spectroscopy

1
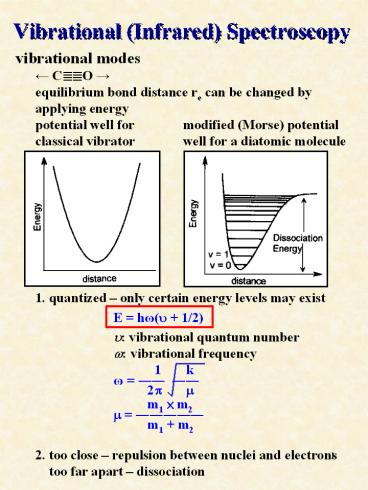
Vibrational (Infrared) Spectroscopy

• vibrational modes
• ? C??O ?
• equilibrium bond distance re can be changed by
• applying energy
• potential well for modified (Morse)
  potential
• classical vibrator well for a diatomic
  molecule
•  
•  
•  
•  
•  
•  
•  
•  
•  
• 1. quantized only certain energy levels may
  exist
• E h?(u 1/2) 
• u vibrational quantum number
• w vibrational frequency

2
ex. HCl u(HCl) 2990 cm-1 DCl
u(DCl) 2145 cm-1 ex. u(NO) bond
order NO 2273 cm-1 3 NO 1880
cm-1 2.5 NO- 1365 cm-1 2 NO2- 886
cm-1 1.5 number of vibrational modes a
molecule consists of N atoms, there are 3N
degrees of freedom translation
rotation vibration nonlinear 3 3
3N 6 linear 3 2
3N 5 type of vibrational modes
stretching mode u bending mode
d IR active absorption Raman active
absorption
3

• frequencies for some commonly encountered groups,
  fragments,
• and linkages in inorganic and organic molecules

4

• ex. W(CO)6
  Mn(CO)5Br
•  
•  
•  
•  
•  
•  
•  
•  
• compound u(CO) (cm-1)
• Ti(CO)62- 1740
• V(CO)6- 1860
• Cr(CO)6 2000
• Mn(CO)6 2095
•  
• stretching modes of CO and IR frequencies
• (a) terminal (b) doubly bridging (c) triply
  bridging
•  
•  

5

• some ligands capable of forming linkage isomers
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•   IR spectrum for nujol
•  
•  
•  
•  
•  
•  
•  

721
1377 1462
2925 2855
6

• symmetry of normal vibrations
• ex. CO32- 6 vibrational modes
• C3(u3a) -1/2u3a 1/2 u3b
• C3(u3b) -3/2u3a - 1/2 u3b
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  

7

• C3
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•   c 0
•   C2

8

• G A1 A2 3E 2A2 E
• 3 translatory modes E, A2
• 3 rotational modes A2, E
• genuine vibrational modes Gg A1 2E A2
  
• IR active E, A2 (3 bands)
• Raman active A1, E (3 bands)
• particular internal coordinates to normal modes
• CO bonds
• E C3 C2 sh S3
  sv
• G 3 0 1 3 0
  1
• GCO A1 E in-plane
  stretching

9

• (i) trans-M(CO)4L2
• D4h E C4 C2 C2 C2 i S4 sh
  sv sd
• L 4 0 0 2 0 0
  0 4 2 0
• OC CO
• OC CO gt A1g B1g Eu
• L IR-active Eu
• (ii) cis-M(CO)4L2
• CO C2v E C2 s s
• OC L 4 0 2 2
  
• OC L gt 2A1 B1 B2
• CO IR-active 2A1, B1,
  B2
•  
• (iii) mer-M(CO)3L3
• CO C2v E C2 s s
• L L 3 1 1
  2
• OC L gt 2A1 B1
• OC IR-active 2A1, B1
•  

10

• (v) M(CO)4L
• L D3v E C3 sv
• 4 1 2
• gt 2A1 E
• IR-active 2A1, E
•  
• D2v E C3 sv sv
• L 4 0 2 2
• gt 2A1 B1 B2
• IR-active 2A1, B1, B2
•  
• (vi) M(CO)3L2
• L D3h E C3 C2 sh S3
  sv
• 3 0 1 3 0
  1
• gt A1 E
• L IR-active E
• L Cs E sh
• 3 1

11

• number of CO stretching bands in IR spetcrum for
  metal carbonyl compounds

12
number of IR bands of some common geometric
arrangements
13

• calculation of force constants
• for diatomic molecule AB harmonic oscillator
• f m-1 l 0
• for polyatomic molecule
• Wilsons method The F and G matrix method
• FG El 0
• F matrix of force constant (potential energy)
• G matrix of masses and spatial relationship of
  
• atoms (kinetic energy)
• E unit matrix 
• e.g. H2O Gg 2A1 B1
• 2 O-H distance Dd1, Dd2 A1 B1
• ?HOH D? A1
• using projection operator to obtain complete
  set
• of symmetry coordinates for vibrations
• A1 S1 D?
• S2 1/v2(Dd1 Dd2)
• B1 S3 1/v2(Dd1 - Dd2)

14

• 2V fd(Dd1)2 fd(Dd2)2 f?(D?)2 2 fdd(Dd1
  Dd2)
• 2 fd?(Dd1 D?) 2 fd?(Dd2 D?)
• Dd1 Dd2 D? fd fdd fd?
  Dd1
• fdd fd fd? Dd2
• fd? fd? f? D?
• sf s
•  
• relationship between the internal coordinates
  and
• the symmetry coordinates
• S U s
• U matrix
• Dq 0 0 1
  Dd1
• Dd1 Dd2 1/v2 1/v2 0
  Dd2
• Dd1 - Dd2 1/v2 -1/v2 0
  Dq
• S U s s U S s (U S) SU
• sfs SFS
• (SU)f(US) SFS
• S(UfU)S SFS gt F UfU
•  

15

• G matrix G UgU
• 0 0 1 gd gdd gd?
  0 1/v2 1/v2
• G 1/v2 1/v2 0 gdd gd
  gd? 0 1/v2 -1/v2
• 1/v2 -1/v2 0 gd? gd? g?
  1 0 0
• g33 v2 g13 0
• v2 g13 g11 g12 0
• 0 0 g11 - g12
• g11 mH mO
• g12 mO cos?
• g13 -(mO/r) sin?
• g33 2(mH mO - mO cos?)/r2
• m reciprocal of the mass
• 2(mH mO - mO cos?)/r2 -(v2mO/r)
  sin? 0
• G -(v2mO/r) sin? mH mO
  (1 cos?) 0
• 0
  0 mH mO (1 - cos?)
•  
• for H2O ? 104.3o31 r 0.9580 Å
• 2.332 -0.0893 0
• G -0.0893 1.0390 0

16

• elements of the g matrix
• mi reciprocal mass of the ith atom
• rij reciprocal of the distance between ith
  and jth

17

• Raman spectroscopy
• light of energy less than that required to
• promote a molecule into an excited electronic
• state is absorbed by a molecule,
• a virtual excited state is created
• virtual state is very short lifetime, the
  majority
• of the light is re-emitted over 360oC, this is
• called Rayleigh scattering
• C. V. Raman found that the energy of a small
• proportion of re-emitted light differs from the
• incident radiation by energy gaps that
• correspond to some of the vibrational modes
• Stokes lines
• anti-Stokes line

18

• schematic representation of Raman spectrometer
• selection rules for vibrational transitions
• a fundamental will be infrared active if the
• normal mode which is excited belongs to the
• same representation as any one or several of
• the Cartesian coordinates
• a fundamental will be Raman active if the
• normal mode involved belongs to the same
• representation as one or more of the
• components of the polarizability tensor of the
• molecule
• the exclusion rule in centrosymmetric
  molecules,

19

• ex. Na2MoO4 dissolved in HCl exhibits Raman
• peaks at 964, 925, 392, 311, 246, 219 cm-1
• 925, 311 cm-1 being polarized
• what can be deduced from the spectrum?
• no n(MoH) and n(OH) bands
• only MCl and MO likely exist
• 964, 925 cm-1 MoO stretching bands
• 392 cm-1 MoO bending mode
• 311, 246, 219 cm-1
• MoCl
  stretching modes
• possible product

20

• normal vibrational modes for common structures

21
(No Transcript)
22
(No Transcript)
23
(No Transcript)
24
(No Transcript)
25
(No Transcript)
26
(No Transcript)