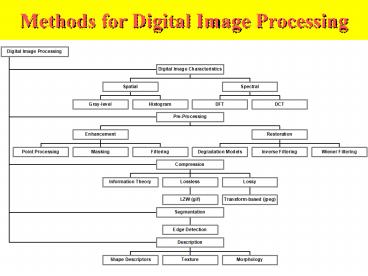
Methods for Digital Image Processing - PowerPoint PPT Presentation
Title:
Methods for Digital Image Processing
Description:
Methods for Digital Image Processing Basic ideas of Image Transforms Spatial Frequency or Fourier Transform Why are Spatial Frequencies important? – PowerPoint PPT presentation
Number of Views:210
Avg rating:3.0/5.0
Title: Methods for Digital Image Processing
1
Methods for Digital Image Processing
2
Basic ideas of Image Transforms
3
Spatial FrequencyorFourier Transform
Jean Baptiste Joseph Fourier
4
Why are Spatial Frequencies important?
- Efficient data representation
- Provides a means for modeling and removing noise
- Physical processes are often best described in
frequency domain - Provides a powerful means of image analysis
5
What is spatial frequency?
- Instead of describing a function (i.e., a shape)
by a series of positions - It is described by a series of cosines
6
What is spatial frequency?
g(x) A cos(x)
g(x)
2?
A
x
7
What is spatial frequency?
A cos(x ? 2?/L) g(x) A cos(x ? 2?/?)
A cos(x ? 2?f)
g(x)
Period (L) Wavelength (?) Frequency f(1/ ?)
Amplitude (A) Magnitude (A)
x
8
What is spatial frequency?
g(x) A cos(x ? 2?f)
g(x)
A
x
(1/f)
period
9
But what if cosine is shifted in phase?
g(x) A cos(x ? 2?f ?)
g(x)
x
?
10
What is spatial frequency?
Let us take arbitrary g(x)
x g(x) 0.00 2 cos(0.25?)
0.707106... 0.25 2 cos(0.50?) 0.0 0.50 2
cos(0.75?) -0.707106... 0.75 2 cos(1.00?)
-1.0 1.00 2 cos(1.25?) -0.707106 1.25 2
cos(1.50?) 0 1.50 2 cos(1.75?)
0.707106... 1.75 2 cos(2.00?) 1.0 2.00 2
cos(2.25?) 0.707106...
g(x) A cos(x ? 2?f ?) A2 m f 0.5 m-1
0.25? 45? g(x) 2 cos(x ? 2?(0.5) 0.25?)
2 cos(x ? ? 0.25?)
We calculate discrete values of g(x) for various
values of x
We substitute values of A, f and ?
11
What is spatial frequency?
g(x) A cos(x ? 2?f ?)
g(x)
We calculate discrete values of g(x) for various
values of x
x
12
Now we take discrete values of Ai , fi and ?i
gi(x) Ai cos(x ? 2?fi ?i), i 0,1,2,3,...
x
13
Now we substitute fi i/N
gi(x) Ai cos(x ? 2?fi ?i), i 0,1,2,3,...
gi(x) Ai cos(x ? 2?i/N ?i), i
0,1,2,3,,N-1 fi/N
N time interval
14
Values for various values of i
gi(x) Ai cos(x ? 2?i/N ?i), i
0,1,2,3,,N-1 fi/N
We calculate values of function for various
values of i
15
Substituting various values of i to the formula
we get various cosinusoides
gi(x) Ai cos(x ? 2?i/N ?i), i 0,1,2,3,,N-1
A2
A1
A0
i1
i2
i0
16
Changing N to N/2
gi(x) Ai cos(x ? 2?i/N ?i), i
0,1,2,3,,N/2 - 1
If N equals the number of pixel in a line, then...
iN/2 - 1
i0
Lowest frequency Highest
frequency
17
What is spatial frequency?
gi(x) Ai cos(x ? 2?i/N ?i), i
0,1,2,3,,N/2-1
If N equals the number of pixels in a line,
then...
iN/2-1
i0
Lowest frequency Highest
frequency
18
What will happen if we take N/2?
gi(x) Ai cos(x ? 2?i/N ?i), i
0,1,2,3,,N/2-1
If N equals the number of pixel in a line, then...
iN/2
i0
Lowest frequency Too high
Redundant
frequency
19
What is spatial frequency?
g(x) A cos(x ? 2?f ?)
gi(x) Ai cos(x ? 2?i/N ?i), i
0,1,2,3,,N/2-1
20
(No Transcript)
21
(No Transcript)
22
We try to approximate a periodic function with
standard trivial (orthogonal, base) functions
Low frequency
Medium frequency
High frequency
23
We add values from component functions point by
point
24
g(x)
i1
i2
i3
i4
i5
i63
x
0
127
Example of periodic function created by summing
standard trivial functions
25
g(x)
i1
i2
i3
i4
i5
i10
x
0
127
Example of periodic function created by summing
standard trivial functions
26
64 terms
g(x)
10 terms
g(x)
Example of periodic function created by summing
standard trivial functions
27
Fourier Decomposition of a step function (64
terms)
g(x)
i1
i2
i3
i4
i5
Example of periodic function created by summing
standard trivial functions
x
i63
0
127
28
Fourier Decomposition of a step function (11
terms)
g(x)
i1
i2
i3
Example of periodic function created by summing
standard trivial functions
i4
i5
i10
x
0
63
29
Main concept summation of base functions
Any function of x (any shape) that can be
represented by g(x) can also be represented by
the summation of cosine functions
Observe two numbers for every i
30
Information is not lost when we change the domain
Spatial Domain
gi(x) 1.3, 2.1, 1.4, 5.7, ., i0,1,2N-1
N pieces of information
Frequency Domain
N pieces of information N/2 amplitudes (Ai,
i0,1,,N/2-1) and N/2 phases (?i, i0,1,,N/2-1)
and
31
What is spatial frequency?
Information is not lost when we change the domain
gi(x)
and
Are equivalent They contain the same amount of
information
The sequence of amplitudes squared is the SPECTRUM
32
EXAMPLE
33
Substitute values
A cos(x?2?i/N) frequency (f) i/N wavelength (p)
N/I N512 i f p 0 0
infinite 1 1/512 512 16 1/32
32 256 1/2 2
Assuming N we get this table which relates
frequency and wavelength of component functions
34
More examples to give you some intuition.
35
Fourier Transform Notation
- g(x) denotes an spatial domain function of real
numbers - (1.2, 0.0), (2.1, 0.0), (3.1,0.0),
- G() denotes the Fourier transform
- G() is a symmetric complex function
- (-3.1,0.0), (4.1, -2.1), (-3.1, 2.1), (1.2,0.0)
, (-3.1,-2.1), (4.1, 2.1), (-3.1,0.0) - Gg(x) G(f) is the Fourier transform of g(x)
- G-1() denotes the inverse Fourier transform
- G-1(G(f)) g(x)
36
Power Spectrum and Phase Spectrum
complex
Complex conjugate
- G(f)2 G(f)?G(f) is the power spectrum of
G(f) - (-3.1,0.0), (4.1, -2.1), (-3.1, 2.1),
(1.2,0.0),, (-3.1,-2.1), (4.1, 2.1) - 9.61, 21.22, 14.02, , 1.44,, 14.02, 21.22
- tan-1Im(G(f))/Re(G(f)) is the phase spectrum of
G(f) - 0.0, -27.12, 145.89, , 0.0, -145.89, 27.12
37
1-D DFT and IDFT
- Discrete Domains
- Discrete Time k 0, 1, 2, 3, , N-1
- Discrete Frequency n 0, 1, 2, 3, , N-1
- Discrete Fourier Transform
- Inverse DFT
Equal frequency intervals
n 0, 1, 2,.., N-1
k 0, 1, 2,.., N-1
38
Fourier 2D Image Transform
39
Another formula for Two-Dimensional Fourier
Image is function of x and y
A cos(x?2?i/N) B cos(y?2?j/M) fx u i/N, fy
v j/M
Lines in the figure correspond to real value 1
Now we need two cosinusoids for each point, one
for x and one for y
Now we have waves in two directions and they have
frequencies and amplitudes
40
Fourier Transform of a spot
Original image
Fourier Transform
41
Transform Results
image
transform
spectrum
42
Two Dimensional Fast Fourier in Matlab
43
Filtering in Frequency Domain
will be covered in a separate lecture on
spectral approaches..
44
- H(u,v) for various values of u and v
- These are standard trivial functions to compose
the image from
45
(No Transcript)
46
lt
lt
image
..and its spectrum
47
Image and its spectrum
48
Image and its spectrum
49
Image and its spectrum
50
Convolution Theorem
Let g(u,v) be the kernel Let h(u,v) be the
image G(k,l) DFTg(u,v) H(k,l)
DFTh(u,v) Then
This is a very important result
where means multiplication and means
convolution.
This means that an image can be filtered in the
Spatial Domain or the Frequency Domain.
51
Convolution Theorem
Let g(u,v) be the kernel Let h(u,v) be the
image G(k,l) DFTg(u,v) H(k,l)
DFTh(u,v) Then
Instead of doing convolution in spatial domain
we can do multiplication In frequency domain
Multiplication in spectral domain
Convolution in spatial domain
where means multiplication and means
convolution.
52
v
Image
u
Spectrum
Noise and its spectrum
Noise filtering
53
Image
v
u
54
(No Transcript)
55
Image of cow with noise
56
white noise
white noise spectrum
kernel spectrum (low pass filter)
red noise
red noise spectrum
57
Filtering is done in spectral domain. Can be very
complicated
58
Image Transforms
- Fast Fourier
- 2-D Discrete Fourier Transform
- Fast Cosine
- 2-D Discrete Cosine Transform
- Radon Transform
- Slant
- Walsh, Hadamard, Paley, Karczmarz
- Haar
- Chrestenson
- Reed-Muller
59
Discrete Cosine Transform (DCT)
- Used in JPEG and MPEG
- Another Frequency Transform, with Different Set
of Basis Functions
60
Discrete Cosine Transform in Matlab
61
Statistical Filters
- Median Filter also eliminates noise
- preserves edges better than blurring
- Sorts values in a region and finds the median
- region size and shape
- how define the median for color values?
62
Statistical Filters Continued
- Minimum Filter (Thinning)
- Maximum Filter (Growing)
- Pixellate Functions
Now we can do this quickly in spectral domain
63
- Thinning
- Growing
64
Pixellate Examples
65
DCT Features
Can be used for face recognition, tell my story
from Japan.
Fringe Pattern
DCT Coefficients
DCT
Zonal Mask
(1,1) (1,2) (2,1) (2,2) . . .
Artificial Neural Network
Feature Vector
66
Noise Removal
Transforms for Noise Removal
Image with Noise Transform
Image reconstructed
67
Image Segmentation Recall Edge Detection
Now we do this in spectral domain!!
68
Image Moments
2-D continuous function f(x,y), the moment of
order (pq) is
Central moment of order (pq) is
69
Image Moments (contd.)
Normalized central moment of order (pq) is
A set of seven invariant moments can be derived
from gpq
Now we do this in spectral domain!!
70
Image Textures
Now we do this in spectral domain!!
The USC-SIPI Image Database http//sipi.usc.edu/
71
Problems
- There is a lot of Fourier and Cosine Transform
software on the web, find one and apply it to
remove some kind of noise from robot images from
FAB building. - Read about Walsh transform and think what kind of
advantages it may have over Fourier - Read about Haar and Reed-Muller transform and
implement them. Experiment
72
Sources
- Howard Schultz, Umass
- Herculano De Biasi
- Shreekanth Mandayam
- ECE Department, Rowan University
- http//engineering.rowan.edu/shreek/fall01/dip/
http//engineering.rowan.edu/shreek/fall01/dip/la
b4.html
73
Image Compression
- Please visit the website
- http//www.cs.sfu.ca/CourseCentral/365/li/material
/notes/Chap4/Chap4.html