Design Example 6.3 Bridge Design - PowerPoint PPT Presentation
1 / 38
Title:
Design Example 6.3 Bridge Design
Description:
The loads a bridge structure must support & pin supports ... bridges, such as the Golden Gate Bridge, consist of cable-suspended spans supported by towers: ... – PowerPoint PPT presentation
Number of Views:994
Avg rating:3.0/5.0
Title: Design Example 6.3 Bridge Design
1
Design Example 6.3 Bridge Design
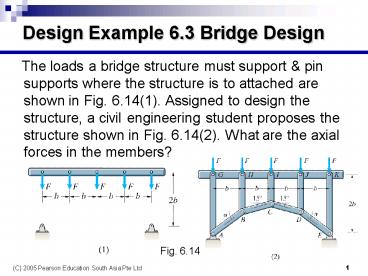
- The loads a bridge structure must support
pin supports where the structure is to attached
are shown in Fig. 6.14(1). Assigned to design the
structure, a civil engineering student proposes
the structure shown in Fig. 6.14(2). What are the
axial forces in the members?
Fig. 6.14
2
Design Example 6.3 Bridge Design
- Strategy
- The vertical members AG, BH, CI, DJ EK are
subjected to compressive forces of magnitude F.
Because of the symmetry of the structure, we can
determine the axial loads in the remaining
members by analyzing joints C B.
3
Design Example 6.3 Bridge Design
- Solution
- We will it as an exercise to show by drawing
the free-body diagrams of joint C that members BC
CD are subjected to equal compressive loads of
magnitude 1.93F. - We draw the free-body diagramof joint B where
TBC ? 1.93F
4
Design Example 6.3 Bridge Design
- Solution
- From the equilibrium equations
- S Fx ?TAB cos ? TBC cos 15 0
- S Fy ?TAB sin ? TBC sin 15 ? F 0
- We obtain TAB ?2.39F ? 38.8. By symmetry,
- TDE TAB. The axial forces in the members are
- shown in Table 6.1
Table 6.1
5
Design Example 6.3 Bridge Design
- Design Issues
- The bridge was an early application of
engineering - The basic difficulty in bridge design is that a
single beam extended between the banks will fail
if the distance between banks, or span, is too
large - To meet the need for bridges of increasing
strength span, civil engineers created
ingenious aesthetic designs in antiquity
continue to do so today
6
Design Example 6.3 Bridge Design
- Design Issues
- The bridge structure proposed by the student in
this example, called an arch, is an ancient
design - Notice in Table 6.1 that all the members of the
structure are in compression - Because masonry (stone, brick or concrete) is
weak in tension but very strong in compression,
many bridges made of these materials were
designed with arched span in the past
7
Design Example 6.3 Bridge Design
- Design Issues
- For the same reason, modern concrete bridges are
often built with arched spans
8
Design Example 6.3 Bridge Design
- Design Issues
- Unlike the masonry, wood steel can support
substantial forces in both compression tension - E.g. the forces in Fig. 6.14(1) can be supported
by the Pratt truss
9
Design Example 6.3 Bridge Design
- Design Issues
- Its members are subjected to both tension
compression (Table 6.2)
Table 6.2
10
Design Example 6.3 Bridge Design
- Design Issues
- The Forth Bridge has a truss structure
- However, truss bridges are too heavy for the
largest bridges. (The Forth Bridge contains 58
000 tons of steel)
11
Design Example 6.3 Bridge Design
- Design Issues
- By taking advantage of the ability of relatively
light cables to support large tensile forces,
civil engineers use suspension structures to
bridge very large spans - The system of 5 forces we are using as an example
can be supported by the simple suspension
structure
12
Design Example 6.3 Bridge Design
- Design Issues
- In effect, the compression arch is inverted
- The loads are suspended from members AB, BC, CD
DE - Every member of this structure except the towers
AG EK is in tension (Table 6.3)
Table 6.3
13
Design Example 6.3 Bridge Design
- Design Issues
- The largest existing bridges, such as the Golden
Gate Bridge, consist of cable-suspended spans
supported by towers
14
6.3 The Method of Sections
- When we need to know the axial forces only in
certain members of a truss, we often can
determine them more quickly using the method of
sections than the method of joints - E.g. consider the Warren truss we used for the
method of joints - It supports loads at B D each member is 2 m
in length - Suppose we need to determine only the axial
force in member BC
15
6.3 The Method of Sections
- Just as in the method of joints, we begin by
drawing a free-body diagram of the entire truss
determining the reactions at the supports - The next step is to cut the members AC, BC BD
to obtain a free-body diagram of a part, or a
section, of the truss
16
6.3 The Method of Sections
- Summing moments about point B, the equilibrium
equations for the section are - S Fx TAC TBD TBC cos 60 0
- S Fy 500 N ? 400 N ? TBC sin 60 0
- S Mpoint B (2 sin 60 m)TAC
- ? (2 cos 60 m)(500
N) 0 - Solving them, we obtain TAC 289 N,
- TBC 115 N TBD ?346 N.
17
6.3 The Method of Sections
- Notice how similar this method is to the method
of joints - Both methods involve cutting members to obtain
free-body diagrams of parts of a truss - In the method of joints, we move from joint to
joint, drawing free-body diagrams of the joints
determining the axial forces in the members as we
go - In the method of sections, we try to obtain a
single free-body diagram that allows us to
determine the axial forces in specific members
18
6.3 The Method of Sections
- In our example, we obtained a free-body diagram
by cutting 3 members, including the 1 (member BC)
whose axial force we wanted to determine - In contrast to the method of joints, the forces
on the free-body diagrams used in the method of
sections are not usually concurrent - As in our example, we can obtain 3 independent
equilibrium equations - Although there are exceptions, it is usually
necessary to choose a section that requires
cutting no more than 3 members, or there will be
more unknown axial forces than equilibrium
equations
19
Example 6.4 Applying the Method of Sections
- The truss in Fig. 6.22 supports a 100-kN load.
The horizontal members are each 1 m in length.
Determine the axial force in member CJ state
whether it is in tension or compression.
Fig. 6.22
20
Example 6.4 Applying the Method of Sections
- Strategy
- We need to obtain a section by cutting members
that include member CJ. By cutting members CD, CJ
IJ, we will obtain a free-body diagram with 3
unknown axial forces. - Solution
- To obtain a section, we cut members CD, CJ
IJ draw the free-body diagram of the part of
the truss on the right side of the truss
21
Example 6.4 Applying the Method of Sections
- Solution
From the equilibrium equation S Fy TCJ sin
45 ? 100 kN 0 We obtain TCJ
141.4 kN. The axial force in member CJ is 141.4
kN (T).
22
Example 6.4 Applying the Method of Sections
- Critical Thinking
- We designed this example to demonstrate that the
method of sections can be very advantageous when
you only need to determine the axial forces in
particular members of a truss - Imagine calculating the axial force in member CJ
using the method of joints - But in engineering applications it is usually
necessary to know the axial forces in all the
members of a truss in that case the 2 methods
are comparable
23
Example 6.5 Choosing an Appropriate Section
- Determine the axial forces in members DG BE
of the truss in Fig. 6.23.
Fig. 6.23
24
Example 6.5 Choosing an Appropriate Section
- Strategy
- We cant obtain a section that involves
cutting members DG BE without cutting more than
3 members. However, cutting members DG, BE, CD
BC results in a section with which we can
determine the axial forces in members DG BE.
25
Example 6.5 Choosing an Appropriate Section
- Solution
- Determine the Reactions at the Supports
- Draw the free-body diagram of the entire truss
26
Example 6.5 Choosing an Appropriate Section
- Solution
- From the equilibrium equations
- S Fx Ax 0
- S Fy Ay K ? F ? 2F ? F 0
- S Mpoint A ?LF ? (2L)(2F) ? (3L)F (4L)K 0
- We obtain the reactions Ax 0, Ay 2F K 2F.
27
Example 6.5 Choosing an Appropriate Section
- Solution
- Choose a Section
- We obtain a section by cutting
- members DG, CD, BC BE.
- Because the lines of action of
- TBE, TBC TCD pass through point
- B, we can determine TDG by
- summing moments about B
- S Mpoint B ?L(2F) ? (2L)TDG 0
28
Example 6.5 Choosing an Appropriate Section
- Solution
- The axial force TDG ?F.
- Then from the equilibrium equation
- S Fx TDG TBE 0
- We see that TBE ?TDG F.
- Member DG is in compression member BE is in
- tension.
29
Example 6.5 Choosing an Appropriate Section
- Critical Thinking
- This is a clever example but not 1 that is
typical of problems faced in practice - The section used to solve it might not be obvious
even to a person with experience analyzing
structures - Notice that the free-body diagram of the section
of the truss is statically indeterminate,
although it can be sued to determine the axial
forces in members DG BE
30
6.4 Space Trusses
- We can form a simple 3-D structure by connecting
6 bars at their ends to obtain a tetrahedron - By adding members, we can obtain more elaborate
structures - 3-D structures such as these are called space
trusses if they have joints that do not exert
couples on the members (i.e. the joints behave
like ball socket supports) they are loaded
supported at their joints
31
6.4 Space Trusses
- Space trusses are analyzed by the same methods we
described for 2-D trusses - The only difference is the need to cope with more
complicated geometry - Consider the space truss
- Suppose that the load F ?2i ? 6j ? k (kN)
- The joints A, B C rest on the smooth floor
- Joint A is supported by the corner where the
smooth walls meet joint C rests against the
back wall
32
6.4 Space Trusses
- We can apply the method of joints to this truss
- 1st, we must determine the reactions exerted by
the supports (the floor walls) - Draw the free-body diagram of the entire truss
- The corner can exert 3 components of force at A,
the floor wall can exert 2 components of force
at C the floor can exert a normal force at B
33
6.4 Space Trusses
- Summing the moments about A, we find that the
equilibrium equations, with forces in kN
distances in m, are - S Fx Ax ? 2 0
- S Fy Ay By Cy ? 6 0
- S Fz Az Cz ? 1 0
34
6.4 Space Trusses
- Solving the equations, we obtain the reactions Ax
2 kN, Ay 4 kN, Az 1 kN, By 1 kN, Cy
1 kN Cz 0.
- In this example, we can determine the axial
forces in members AC, BC CD from the free-body
diagram of joint C - To write the equilibrium equations for the joint,
we must express the 3 axial forces in terms of
their components
35
6.4 Space Trusses
- Because member AC lies along the x axis, we
express the force exerted on joint C by the axial
force TAC as the vector ?TACi - Let rCB be the position vector from C to B
- rCB (2 ? 4)i (0 ? 0)j (3 ? 0)k ?2i
3k - Dividing this vector by its magnitude that points
from C toward B yields
36
6.4 Space Trusses
- And we express the force exerted on joint C by
the axial force TCD as the vector - TBC eCB TBC(?0.555i 0.832k)
- In the same way, we express the force exerted on
joint C by the axial force TCD as the vector - TCD(?0.535i 0.802j 0.267k)
- Setting the sum of the forces on the joint equal
to zero, we obtain - ?TACi TBC(?0.555i 0.832k)
- TCD(?0.535i 0.802j 0.267k) (1 kN)j 0
37
6.4 Space Trusses
- And then get 3 equilibrium equations
- S Fx ?TAC ? 0.555TBC ? 0.535TCD 0
- S Fy 0.802TCD 1 kN 0
- S Fz 0.832TBC 0.267TCD 0
- Solving these equations, the axial forces are TAC
0.444 kN, TBC 0.401 kN TCD ?1.247 kN - Members AC BC are in tension member CD is in
compression
38
6.4 Space Trusses
- By continuing to draw free-body diagrams of the
joints, we can determine the axial forces in all
the members - As our examples demonstrates, 3 equilibrium
equations can be obtained from the free-body
diagram of a joint in 3 dimensions, so it is
usually necessary to choose joints to analyze
that are subjected to known forces no more than
3 unknown forces