Tema I: Cinematica

1
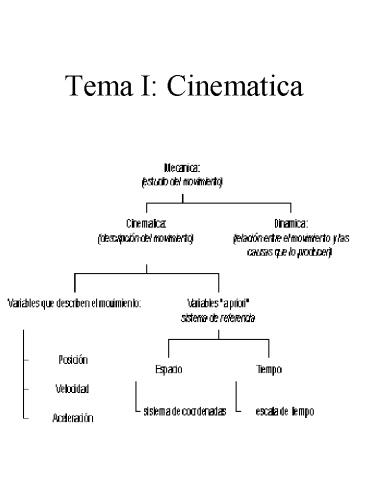
Tema I Cinematica
2
Espacio
P(x,y,z)- representación del punto P en el
sistema de ejes coordenadas cartesianas
ortogonales OXYZ. SI- patron de longitud
METRO. Espacio euclideo tridimensional Se define
la distancia d12 entre P1(x1,y1,,z1) y
P2(x2,y2,z2)
Z
P1
P2
Y
Vector de posición
o
X
Distancia entre P1y P2
Norma (modulo) de un vector
3
Tiempo
Aparato de medir el tiempo RELOJ. SI-
segundos Mecánica clasica tiempo absoluto (no
depende del estado del movimiento del observador
que realiza la medida)
Z
P
z
o
P
Z
Y
?
X
?
(?,?,z) (x,y,z)
Y
P
o
X
Y
?
?
X
o
(r,?,?) (x,y,z)
4
(No Transcript)
5
Def Trayectoria del movil Def Desplazamiento
?r
Z
r(t)
?r
r(t?t)
S.R OXYZ-fijo
O
Y
X
6
Vector Velocidad modulo, sentido y direccion
Def Velocidad promedio
S.R OXYZ-fijo
v
Z
r(t)
?r
vm
r(t?t)
O
Y
X
Def Velocidad instantanea
7
Velocidad en terminos del arco recorrido
S.R OXYZ-fijo
Z
r(t)
?s
Derivación en cadena
?r
Oo
r(t?t)
O
Y
X
Def. de la derivada
Se obtiene para la velocidad en terminos del arco
8
Nota uT y v tienen i) siempre la misma
dirección ii) no siempre el mismo sentido
Z
r(t)
ds
dr
Oo
r(tdt)
O
Y
X
Analizamos 2 casos
Unidades SI -gt m/s
9
Vector Aceleración modulo, sentido y direccion
Def Aceleración promedio
S.R OXYZ-fijo
v(t)
Z
r(t)
?r
a
am
r(t?t)
v(t?t)
O
Y
X
Def Aceleración instantanea
10
Componentes intrinsecas de la acelaración 1.
Aceleración tangencial 2. Acelaración normal
11
Que es
?
Que es la magnitud
?
Pasos para determinar esta magnitud 1. El
movimiento se desarrolla en el plano
oscilador. 2. Los vectores uN para ?t-gt0 se unen
en el punto C, denominado centro de la
curvatura. 3. Se define el radio de la curvatura
? AC 4. Los vectores uT y uN forman el mismo
angulo ?, puesto que tanto en A como en A
12
Representación gráfica
13
Se define el arco
Definir d? en función de
El limite infinitesimal A-gtA, dt-gt0, d?-gt0
uT(A) df
duT uTdf
Si A-gtA
uT(A)
Por lo tanto
14
Entonces se tiene
Responsable del cambio en la magnitud de la
velocidad.
Responsable del cambio de dirección en la
velocidad
Casos particulares 1. vconst -gt aT0 (mov.
uniforme) 2. ?? -gt aN0 (mov. rectilineo)
15
(No Transcript)
16
(No Transcript)
17
(No Transcript)
18
(No Transcript)
19
(No Transcript)
20
Otros casos particulares 1. Movimiento
uniformemente acelerado aTconst (MUA)
21
2. Movimiento rectilineo uniformemente acelerado
aTconst, ? ?, aN0 (MRUA)
22
Movimiento Circular. (MC)
ds
R
O
Unidades de ? rad ?rad/s
23
Movimiento Circular desde el plano de la
particula.
Se considera Una particula en MC. en un circulo
de radio R y centro Oo
Vector velocidad angular 1. Modulo 2. Dirección
y sentido
Vector velocidad en MC
24
Definición de la aceleración angular en (MC)
Caso particular ?const -gt MCUA
Unidades de ? rad ?rad/s ?rad/s2
25
Relación de ? y ? con aT y aN
Si ?const, ?0, aT0 -gt MCU
En general para un MC
26
(No Transcript)
27
(No Transcript)
28
(No Transcript)