Special Case: Paired Sample TTest

1
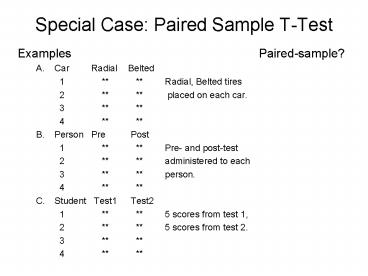
Special Case Paired Sample T-Test

• Examples Paired-sample?
• Car Radial Belted
• 1 Radial, Belted tires
• 2 placed on each car.
• 3
• 4
• Person Pre Post
• 1 Pre- and post-test
• 2 administered to each
• 3 person.
• 4
• Student Test1 Test2
• 1 5 scores from test 1,
• 2 5 scores from test 2.
• 3
• 4

2
Example

• Nine steel plate girders were subjected to two
  methods for predicting sheer strength. Partial
  data are as follows
• Girder Karlsruhe Lehigh difference, d
• 1 1.186 1.061
• 2 1.151 0.992
• 9 1.559 1.052
• Conduct a paired-sample t-test at the 0.05
  significance level to determine if there is a
  difference between the two methods.
• adapted from Montgomery Runger, Applied
  Statistics and Probability for Engineers.

3
Example (cont.)

• Hypotheses
• H0 µD 0
• H1 µD ? 0
• t__________ ______
• Calculate difference scores (d), mean and
  standard deviation, and tcalc
• d 0.2736
• sd 0.1356
• tcalc ______________________________

4
What does this mean?

• Draw the picture
• Decision
• Conclusion

5
Goodness-of-Fit Tests

• Procedures for confirming or refuting hypotheses
  about the distributions of random variables.
• Hypotheses
• H0 The population follows a particular
  distribution.
• H1 The population does not follow the
  distribution.
• Examples
• H0 The data come from a normal distribution.
• H1 The data do not come from a normal
  distribution.

6
Goodness of Fit Tests (cont.)

• Test statistic is ?2
• Draw the picture
• Determine the critical value
• ?2 with parameters a, ? k 1
• Calculate ?2 from the sample
• Compare ?2calc to ?2crit
• Make a decision about H0
• State your conclusion

7
Tests of Independence

• Hypotheses
• H0 independence
• H1 not independent
• Example
• Choice of pension plan.
• 1. Develop a Contingency Table

8
Example

• 2. Calculate expected probabilities
• P(1 n S) _______________ E(1 n S)
  _____________
• P(1 n H) _______________ E(1 n H)
  _____________
• (etc.)

9
Hypotheses

• Define Hypotheses
• H0 the categories (worker plan) are
  independent
• H1 the categories are not independent
• 4. Calculate the sample-based statistic
• ________________________________________
• ______

10
The Test

• 5. Compare to the critical statistic, ?2a, r
• where r (a 1)(b 1)
• for our example, say a 0.01
• ?2_____ ___________
• Decision
• Conclusion

11
Homework for Wednesday, Nov. 10

• pp. 319-323 25, 27
• Pp. 345-346 12, 13

12
Homework