Direction of travel of cossinwt bx waves

1

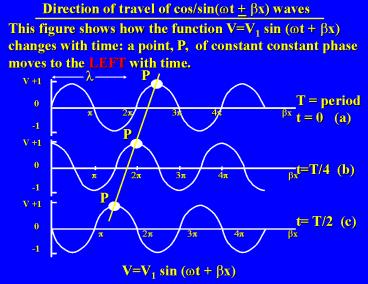
Direction of travel of cos/sin(wt bx) waves
This figure shows how the function VV1 sin (wt
bx) changes with time a point, P, of constant
constant phase moves to the LEFT with time.
P
l
T period t 0 (a) tT/4 (b) t T/2 (c)
P
P
VV1 sin (wt bx)
2

Direction of travel of cos/sin(wt bx) waves
This figure shows how the function VV1 sin (wt -
bx) changes with time a point, P, of constant
constant phase moves to the RIGHT with time.
P
l
V 1 0 -1
T period t 0 (a) tT/4 (b) t T/2 (c)
p 2p 3p
4p bx
P
V 1 0 -1
p 2p 3p
4p bx
P
V 1 0 -1
p 2p 3p
4p bx
VV1 sin (wt - bx)
3
Phase Velocity of a Wave on a Transmission Line

The PHASE VELOCITY of a wave is defined as the
velocity of a point of constant phase. For a
point of constant phase, V is constant, hence
wt bx constant To find
the velocity of this constant phase point we must
obtain ?x/?t, so differentiate the above w.r.t
time, t w b ?x/?t
0 \ PHASE VELOCITY ?x/?t w/b v For a
lossless transmission line with inductance per
unit length L and capacitance per unit length C
Example 2.1 shows that the velocity of a TEM wave
on a transmission line is the same as that of an
EM wave in the dielectric medium of the line.
4
Substituting for ?V/?t and ?2V/?t2 in 7
If V V1 e(jwtgx) then
Comparing (16) and (17), we see that for our
trial function to be a solution
?2V (R jwL)(G jwC)V
gt g2 (R jwL)(G jwC)
(18)
Thus V1 e(jwtgx) is a solution to Equation 7 if
g (R jwL)(G jwC)1/2 (19)

5
The sign again indicates the direction the wave
is travelling in the solution with e-gx
corresponds to a forward travelling wave (x
direction) the solution with egx corresponds to
a backward travelling wave (-x
direction) The general solution is
V V1 e jwt e -gx V2 e jwt e
gx where V1 and V2 are independent arbitrary
amplitudes which depend on the circumstances.

6
Thus for the lossless case egx e jbx
i.e. g is
purely imaginary (? j?). In general, g is
complex and has both real and imaginary parts
g (RjwL)(GjwC)1/2 (a
jb) Hence egx e(ajb)x
eaxejbx The factor eax operates on the
amplitude of the wave, decreasing it
exponentially. a is termed the
ATTENUATION CONSTANT eax gives the amplitude
attenuation as the wave travels ejbx gives the
phase change over distance x
g is termed the PROPAGATION CONSTANT
7
For a forward travelling wave
V V1 e-ax e j(wt-bx)
amplitude factor phase factor
time
variation

8

• Part 2 - Characteristic Impedance and Reflections
• Lecture Topics
• 4. Current and voltage on a transmission
  line
• Characteristic impedance, ZO
  
• Characteristic impedance of lossless
  lines
• Characteristic impedance of general
  lines
• Infinitely long transmission lines
  
• Reflections on transmission lines
• 5. Transmission line with change of ZO
  voltage
• reflection coefficient
• Voltage reflection coefficient at an
  arbitrary
• distance l from the load ZL
• 6. Impedances of terminated lines
• Voltage Standing Wave Ratio (VSWR)
  
• Voltage Standing Wave measurement

9

• Example 3.2 - High-frequency expressions for the
  attenuation and phase constants, a and b.

Determine approximate expressions for a and b
when w is large (i.e. at high frequencies) or
when R and G are small.
10

• Example 3.3 - Calculation of a and b.
• For a parallel wire transmission line the
  primary line constants at 3 kHz are
• R 6.74 W/km
• L 0.00352 H/km
• G 0.29x10-6 S/km
• C 0.0087x10-6 F/km
• Find the attenuation and phase constants (a and
  b) and the phase velocity of the line at 3
  kHz. Find also the distance at which the wave
  amplitude has decayed to 0.1 of its initial value.

11

• Example 3.4 - The Heaviside Condition
• Show that there will be no distortion on a
  transmission line for which R/L G/C (the
  Heaviside Condition), provided L and C do
  not depend on frequency.

Oliver Heaviside (1850 - 1925) English physicist
and electrical engineer Started career as a
telegrapher Nominated for a Nobel Prize Also
known for predicting the "Heaviside
Layer" in the atmosphere
12
Current on a transmission line

So far we have mainly considered the voltage on a
transmission line V V1e jwte-gx V2e
jwtegx g (RjwL)(GjwC)1/2 The
instantaneous voltage at any given point is the
SUM of the forward and backward wave
voltages. Consider the current in the line - if
V is sinusoidal, I must also be sinusoidal (if we
are working in a linear system, I ? V) hence the
total current will have the same form as the
total voltage V
V1e jwte-gx V2e jwtegx (1)
I I1 ejwte-gx I2 e jwtegx
where I1 , I2 are the current amplitudes.

N.B. minus sign because the currents are
flowing in opposite directions
13
From the Telegrapher's Equations

But I I1 ejwte-gx I2 e jwtegx ,
so ?I/?t j?I1 ejwte-gx j?I2 e jwtegx
jwI Hence

• Similarly, V V1e jwte-gx V2e jwtegx , so
• ?V/?x -?V1e jwte-gx ?V2e jwtegx
• Hence
• -gV1ejwte-gx gV2ejwtegx -(R
  jwL)I

14
-gV1ejwte-gx gV2ejwtegx -(R
jwL)I Re-arranging for I

• But I I1 ejwte-gx
  I2 e jwtegx
• where I1 and I2 are the amplitudes of the forward
  and backward current waves respectively.

15
Hence
Note that Zo is NOT per unit length - units are
just W.

The forward and backward current waves (I, I-)
are related to the respective forward and
backward voltage waves (V, V-) by the
CHARACTERISTIC IMPEDANCE, Zo.
16
Characteristic Impedance of a Lossless Line

For a lossless line R0 and G0 hence
In the lossless case, Zo is purely REAL, i.e.
resistive.
Characteristic Impedance of a General
Transmission Line
If the losses are small, i.e. R ltlt w L and G ltlt w
C then Zo can be approximated by
17
Note that for a general transmission line Zo will
be a complex impedance unless the Heaviside
Condition is met, i.e. unless R/L G/C. In this
case, once again

which is the same as for a lossless line . . . .
but the line will NOT be lossless in this case
because R g 0 and G g 0.
Some General Points Regarding Characteristic
Impedance 1. Note that the characteristic
impedance relates the forward voltage wave V to
the forward current wave I OR the backward
voltage wave V- to the backward current wave I-
18

• 2. It does NOT relate the TOTAL voltage to the
  TOTAL current

Except in the special case when there is only a
forward wave on the line (i.e. V- 0 and I-
0)
3. N.B. Zo is NOT the impedance you would
measure simply by connecting the line to an
impedance measuring system this would give you
the open-circuit impedance Zoc. We will see later
(Example 5.2) that
Zo (ZocZsc)1/2 where Zsc is the
short-circuit impedance.
19

• Example 4.1 - Characteristic impedance of a
  parallel-wire line.
• Calculate the characteristic impedance of a
  lossless,
• air-spaced, two-wire transmission line for which
  the wire radius is 0.5 mm and the spacing is 5
  mm.

20

• Example 4.2 - Characteristic impedance of a
  coaxial line.
• A coaxial, lossless transmission line with an
  inner conductor of diameter 2 mm and internal
  diameter for the exterior conductor of 7.5 mm is
  filled with polythene dielectric (er
  2.56). Calculate the characteristic impedance
  of the line.

21
INFINITELY LONG TRANSMISSION LINES If
we have a forward wave propagating down a
transmission line of finite length, any
discontinuities present on the line will give
rise to reflections, i.e. backward waves. But
for an infinite, uniform transmission line there
are no discontinuities and so no reflections -
the total voltage and total current at any point
on the line (including the input end) will be
given by

So the infinite line just looks like a load Zo to
the source
I
I
Zo
V
V
Characteristic impedance Zo
22
Reflections on Transmission
Lines q Like other waves, voltage and current
waves on transmission lines can be reflected. q
They are reflected by discontinuities on the
line, e.g. the load at the end of the line or a
changeover from one type of line to another.
ZL

23
q A transmission line with
discontinuities will have backward (or
reflected) waves when a forward wave is
propagated along it. q Consequently the TOTAL
voltage and current on the line will be VT
V V- and IT I I-
VT / IT g Zo

• q The impedance seen by the source (i.e. VT/IT
  at the input terminals of the line) will depend
  on the magnitude and phase of these reflections.
• q Since there is a power flow associated with
  each of the forward and backward waves, the
  power delivered to the load at the end of the
  transmission line will drop if there are
  reflections.
• When there are no
  reflections the
• power delivered to the load is
  maximised.

24
How can the reflections be prevented?

Previously we have seen that (a) an infinite
transmission line of characteristic impedance Zo
behaves as an effective load of impedance Zo
. (b) there are no reflections on an infinite
transmission line.
A B
finite A length B
infinite
Zo Zo
Zo Zo
Hence, for no reflections and maximum power
transfer a line of characteristic impedance Zo
should be terminated in a load Zo . In this case
the load and line are said to be MATCHED.
25
Summary

q The forward and backward currents are related
to the forward and backward voltages by Zo, the
CHARACTERISTIC IMPEDANCE.
q For a lossless line (R0, G0) or for one that
obeys the Heaviside Condition (R/LG/C)
26
q If there is a reflected wave on the line then

q Reflected waves are caused by DISCONTINUITIES
on a transmission line, e.g. the end of the line
or a changeover from one type of cable to
another.
ZL

q There are NO REFLECTED WAVES on an INFINITELY
LONG TRANSMISSION LINE.
27
q An infinitely long transmission line of
characteristic impedance Zo looks to the source
like a load Zo connected directly to it.
q MAXIMUM POWER TRANSFER to the load occurs when
there are NO REFLECTIONS ON THE LINE.
q To achieve this the load and line must be
MATCHED, i.e. the load impedance must be the same
as the characteristic impedance of the line.
Zo
ZL Zo