4'3 The Fundamental Theorem of Calculus

1
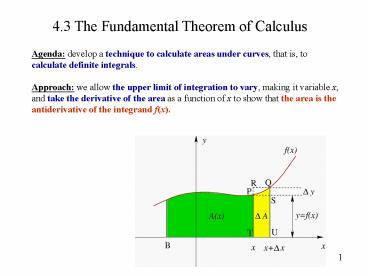
4.3 The Fundamental Theorem of Calculus
Agenda develop a technique to calculate areas
under curves, that is, to calculate definite
integrals. Approach we allow the upper limit
of integration to vary, making it variable x, and
take the derivative of the area as a function of
x to show that the area is the antiderivative of
the integrand f(x).
1
2
The integral with a variable upper limit of
integration is a function of the position of this
limit We change this position by Dx and
determine the change in the area DA and then
apply the four-step process to calculate the
derivative.
area PSUT DA area RQUT TP Dx DA UQ Dx
2
3
Thus, A(x) is an atiderivative of the function
f(x). Recalling our old notation for the
antiderivative, we write Note the constant of
integration C inside F(x) reflects the fact that
the boundary B may be chosen differently. Corolla
ry the area under the curve between the
verticals xB and xa is
, and between the verticals xB and xb is
. Then, the difference
between them is the area between the verticals
xa and xb
3
4
Fundamental Theorem of Calculus If f is
continuous on the interval a,b, then Where,
F is a function such that Ff on a,b - that
is, F is an antiderivative of f. Additional
notation antiderivative is also denoted as
and called the indefinite
integral. Exercises Find each area bounded by
indicacted curves and x-axis
4
5
Homework Section 4.3 1,3,5,7,9.
5