Chap 7 Energy Band
1 / 27
Title: Chap 7 Energy Band
1
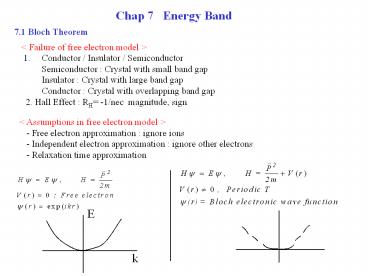
Chap 7 Energy Band
7.1 Bloch Theorem
lt Failure of free electron model gt
- Conductor / Insulator / Semiconductor
- Semiconductor Crystal with small band gap
- Insulator Crystal with large band gap
- Conductor Crystal with overlapping band gap
- 2. Hall Effect RH -1/nec magnitude, sign
lt Assumptions in free electron model gt - Free
electron approximation ignore ions -
Independent electron approximation ignore other
electrons - Relaxation time approximation
E
k
2
- Blochs Theorem
3
Periodic Boundary Condition
4
Proof of Block Theorem Any function obeying
Born-von Karman B.C. can be expanded as
5
Equivalent to Schrodinger equation written in
momentum space.
6
- Significance of k-label
7
7.2 Explicit write out of the central equation
Schrodinger Equation Central
Equation
8
(No Transcript)
9
Note 1) To have a non-trivial solution, the
determinent should vanish. Give Eigenvalue
Ek.n k the wave vector that labels Ck n
the index for the order of energy (band
index) 2) If we had started with kg instead of
k, we would have obtained the same set of
eigenvalues. Hence we can restrict k values
in the first Brillouin Zone
Reduced Zone Scheme
10
Quantum perturbation theory
Most important
-G/2
G/2
11
- Empty Lattice (V0), Free electron
Example ) Low-lying free electron bands of a
simple cubic lattice along the 100 direction
12
(No Transcript)
13
(No Transcript)
14
7.3 Band Calculations
Approximate solution at a zone boundary under a
weak periodic potential
- At the zone boundary, a bandgap is created
- Band gap Forbidden energy range
- electrons in a crystal cannot have energy value
in this range
15
Eigenstate (Blochs wave function)
Free electron Traveling wave
Crystal electron Standing wave
16
Physical origin of the band gap
Electron density
V is generally negative Bragg Diffraction
standing wave eigenstate different spatial
charge distribution gt difference in potential
energy gt band gap
17
- Solution of Blochs equation near a zone boundary
When k is near the zone boundary, then the
central equation becomes,
18
Hence the band energy varies as quadratic in
k-tilda as we move away from the zone boundary
19
Metals and Insulators
Free electron
Second band
First band
- Insulators Electrons exactly fill one or more
bands
External electric field will not cause current
flow since the band is separated by the band gap.
- Metals Electrons partially fill one or more
bands
metal
insulator
metal
20
7.4 Equation of Motion
1). Electron velocity ltvgt
Velocity of a wave packet Group velocity
2). Equation of Motion
Response of electrons under external force
Blochs theorem
21
- Fext External Force ? Hamiltonian
HH0-Fx - H, T H -Fx, T -Fx, T -FxTTFx
TFxF(xa)TFxTFaT - H,TFaT
22
- Hand waving argument
Group velocity
Traveling speed of a wave packet
23
- Physical Force
- In DC electric field,
Fext -eE
24
E, v
velocity
p/a
Energy
- In Magnetic field,
25
7.5 Effective Mass
- Mass ratio of force to acceleration
F total force m electron mass a electron
acceleration
F ma
- Effective mass ratio of external force to
acceleration
1/m determines curvature of E(k) .
Free electron
26
E, v
Negative mass
Positive mass
p/a
Force
acceleration
Light electron
Heavy electron
27
Nearly Free electron band
E
In a typical semiconductor, l 5eV, V
0.11eV m/m 0.10.01
p/a