Connectivity

1
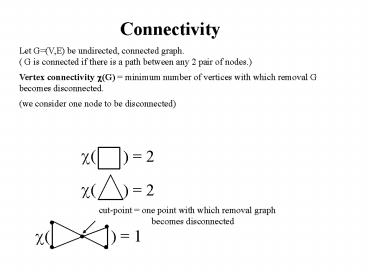
Connectivity
Let G(V,E) be undirected, connected graph. ( G
is connected if there is a path between any 2
pair of nodes.) Vertex connectivity ?(G)
minimum number of vertices with which removal G
becomes disconnected. (we consider one node to be
disconnected)
?(
) 2
?(
) 2
cut-point one point with which removal graph
becomes disconnected
?(
) 1
2
Connectivity
Edge connectivity ?(G) minimum number of edges
with which removal G becomes disconnected.
?(
) 2
bridge
?(
) 2
?(
) 1
Theorem ?(G) ? ?(G) Proof Let ?(G)
?, ?(G) ?. Let L ? V s.t. G(V, E \ L)
disconnected, G K1? K2 For any vertex e ? L
take one end point (and remove it) ? we removed
L ? V vertices G(V \ L, E) is also
disconnected ? ? ? ?
3
Connectivity
Theorem ?(G) ? ?(G) ? ?(G)
(?(G) minimum degree of G)
bridge
?(
) 1
?(
) 2
cut-point
4
2 - connected graphs
1-connected graph - has cut-point (tree both 1
edge and 1 node connected) Minimal 2-connected
graph - deleting of any edge or node makes graph
1-connected Example only cycles
by removing this edge graph would still be
2-connected, but not minimal 2-connected
Theorem G is 2-connected ? any 2 vertices belong
to a simple cycle. (simple
cyclecycle without self-
intersection) Proof ?) - if we remove any 1
node on the path, graph is still connected
(because is 2-connected)
5
2 - connected graphs
b
a
black line two completely disjoint paths from
a to b ?) Proof is by contradiction. Assume G is
1-connected. Let any a,b belong to simple cycle.
Assume there is v?V s.t. G\v is disconnected.
Then there exist 2 vertices a and b between a
path between them, which is a contradiction
(because if a,b belong to a simple cycle, if we
remove any node graph is still connected)
6
Blocks
Block 2-connected maximal component
( maximal 2-connected subgraph od G ) Example
2 blocks (we assume that 1 edge is
1-connected)
4 blocks (maximal 2-comp.) -we may present
each block as a triangle -different blocks do not
share edges -in Intro. To Algorithms-algorithm
for finding bi-connectivity of a graph
7
Finding blocks
DFS (depth first search) - main problem how to
identify cut-points in a graph DFS graph is
undirected, for a purpose of the alg., assume
each edge consists of 2 edges and
cut-point
0 - nodes we didnt visit 1 - nodes we visited 2
- nodes with no outgoing edges
12
3 blocks
2
21
2
2
2
1
- detecting a cycle if weve already visited a
node, there is a cycle
8
Mengers Theorem
(vertex connectivity) Theorem G is ?-connected ?
for any 2 points a,b there are ? vertex
disjoint paths.
?
a
b
Max. of paths ? min. of separation
points
b
a
? vertex disjoint paths (do not share any points)
very important thm. (in flow theory)
9
3-connected graphs

• (vertex connectivity)
• at least 3 nodes need to be removed to make the
  graph disconnected
• connection with planarity
• Properties of 3-connected planar graphs

3
outer planar all nodes on outer
face
234
2
4
1245
123456
1
5
156
6
2-connected
10
3-connected graphs
different embeddings of abstract graph in the
plane
2
234
2
4
4
3
3
123456
12345
1
1
5
5
156
6
6

• 3-connected graphs have only 1 embedding

11
3-connected graphs

• smallest 3-connected graph
• smallest 2-connected graph
• smallest non-trivial 3-connected graph

4
2
234
124
1
3
1
3
124
234
2
123
4
134
123
143
unique embedding
3-paths between any two points (Mengers Theorem)
12
3-connected graphs
2
3
6
1
5
4
octahedron (8 faces) dual cube
only 1 embedding