Basic Gene Expression Data AnalysisClustering

1
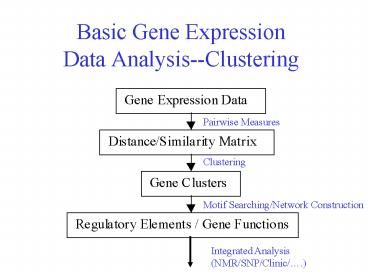
Basic Gene Expression Data Analysis--Clustering
Pairwise Measures
Clustering
Motif Searching/Network Construction
Integrated Analysis (NMR/SNP/Clinic/.)
2
Microarray Experiment
3
Collections of Experiments

• Time course after a treatment
• Different treatments
• Disease cell lines
• Data are represented in a matrix

4
Cluster Analysis

• Grouping of genes with similar expression
  profiles
• Grouping of disease cell lines/toxicants with
  similar effects on gene expression
• Clustering algorithms
• Hierarchical clustering
• Self-organizing maps
• K-means clustering

5
Gene Expression Clustering
Normalized Expression Data
Protein/protein complex
Semantics of clusters From co-expressed to
co-regulated
DNA regulatory elements
6
Key Terms in Cluster Analysis

• Distance Similarity measures
• Hierarchical non-hierarchical
• Single/complete/average linkage
• Dendrograms ordering

7
Measuring Similarity of Gene Expression

• Euclidean (L2) distance
• Manhattan (L1) distance
• Lm (x1-x2my1-y2m)1/m
• L8 max(x1-x2,y1-y2)
• Inner product x1x2y1y2
• Correlation coefficient
• Spearman rank correlation coefficient

(x2,y2)
(x1, y1)
8
Distance Measures Minkowski Metric
ref
9
Commonly Used Minkowski Metrics
10
An Example
x
3
y
4
11
Manhattan distance is called Hamming distance
when all features are binary.
Gene Expression Levels Under 17 Conditions
(1-High,0-Low)
12
From Clustering to Correlation
Expression Level
Expression Level
Gene A
Gene B
Gene B
Gene A
Time
Time
Expression Level
Gene B
Gene A
Time
13
Similarity Measures Correlation Coefficient
14
Hierarchical Clustering
Given a set of N items to be clustered, and an
NxN distance (or similarity) matrix, the basic
process hierarchical clustering is this
1.Start by assigning each item to its own
cluster, so that if you have N items, you now
have N clusters, each containing just one item.
Let the distances (similarities) between the
clusters equal the distances (similarities)
between the items they contain. 2.Find the
closest (most similar) pair of clusters and merge
them into a single cluster, so that now you have
one less cluster. 3.Compute distances
(similarities) between the new cluster and each
of the old clusters. 4.Repeat steps 2 and 3
until all items are clustered into a single
cluster of size N.
15
Hierarchical Clustering
Normalized Expression Data
16
Hierarchical Clustering
3 clusters?
2 clusters?
17
Cluster Analysis

• Eisen et al. (1998) (PNAS, 9514863)

• Correlation as measure of co-expression

Experiment over time
18
Cluster Analysis

• Scan matrix for maximum

• Join genes to 1 node

• Update matrix

19
Cluster Analysis

• Result Dendogram assemling N genes
• Points of discussion
• similarity based, useful for co-expression
• dependent on similarity measure?
• useful in preliminary scans
• biological relevance of clusters?

20
Distance Between Two Clusters

• single-link clustering (also called the
  connectedness or minimum method) we consider
  the distance between one cluster and another
  cluster to be equal to the shortest distance from
  any member of one cluster to any member of the
  other cluster. If the data consist of
  similarities, we consider the similarity between
  one cluster and another cluster to be equal to
  the greatest similarity from any member of one
  cluster to any member of the other cluster.
• complete-link clustering (also called the
  diameter or maximum method) we consider the
  distance between one cluster and another cluster
  to be equal to the longest distance from any
  member of one cluster to any member of the other
  cluster.
• average-link clustering we consider the
  distance between one cluster and another cluster
  to be equal to the average distance from any
  member of one cluster to any member of the other
  cluster.

• Single-Link Method / Nearest Neighbor
• Complete-Link / Furthest Neighbor
• Their Centroids.
• Average of all cross-cluster pairs.

21
Single-Link Method
Euclidean Distance
a
a,b
b
a,b,c
a,b,c,d
c
c
d
d
d
(1)
(3)
(2)
Distance Matrix
22
Complete-Link Method
Euclidean Distance
a
a,b
a,b
b
a,b,c,d
c,d
c
c
d
d
(1)
(3)
(2)
Distance Matrix
23
Identifying disease genes
X. Chen P.O. Brown et al Molecular Biology of
the Cell Vol. 13, 1929-1939, June 2002
24

• Human tumor patient and normal cells various
  conditions
• Cluster or Classify genes according to tumors
• Cluster tumors according to genes

25
K-Means Clustering Algorithm

• 1) Select an initial partition of k clusters
• 2) Assign each object to the cluster with the
  closest center
• 3) Compute the new centers of the clusters
• 4) Repeat step 2 and 3 until no object changes
  cluster

26
K-Means Clustering
This method initially takes the number of
components of the population equal to the final
required number of clusters. In this step itself
the final required number of clusters is chosen
such that the points are mutually farthest apart.
Next, it examines each component in the
population and assigns it to one of the clusters
depending on the minimum distance. The centroid's
position is recalculated everytime a component is
added to the cluster and this continues until all
the components are grouped into the final
required number of clusters.

• Basic Ideas using cluster centre (means) to
  represent cluster
• Assigning data elements to the closet cluster
  (centre).
• Goal Minimise square error (intra-class
  dissimilarity)
• Variations of K-Means
• Initialisation (select the number of clusters,
  initial partitions)
• Updating of center
• Hill-climbing (trying to move an object to
  another cluster).

27
The K-Means Clustering Method

• Example

28
k-means Clustering Procedure (1)
Initialization 1 Specify the number of cluster k
for example, k 4
Expression matrix
Each point is called gene
29
k-means Clustering Procedure (2)
Initialization 2 Genes are randomly assigned to
one of k clusters
30
k-means Clustering Procedure (2)
Calculate the mean of each cluster
(6,7)
(3,4)
(3,2)
(1,2)
31
k-means Clustering Procedure (4)
Each gene is reassigned to the nearest cluster
32
k-means Clustering Procedure (4)
Each gene is reassigned to the nearest cluster
33
k-means Clustering Procedure (5)
Iterate until the means are converged
34
k-means clustering application

Result 13 clusters of 30 clusters had
statistical significance for each biological
function
S. Tavazoie GM Church Nature Genetics Vol. 22,
July 1999
35
Computation Time and Memory Requirementn genes
and m experiments

• Computation time
• Hierarchical clustering
• O( m n2 log(n) )
• K-means clustering
• t number of iterations
• O( k t m n )

• Memory requirement
• Hierarchical clustering
• O( mn n2 )
• K-means clustering
• t number of iterations
• O( mn kn )

36
Issues in Cluster Analysis

• A lot of clustering algorithms
• A lot of distance/similarity metrics
• Which clustering algorithm runs faster and uses
  less memory?
• How many clusters after all?
• Are the clusters stable?
• Are the clusters meaningful?

37
K-Means vs Hierarchical Clustering
38
Pattern Recognition

• Clarification of decision making processes and
  automating them using computers

supervised
unsupervised

• unknown number of classes

• known number of classes

• based on a training set

• no prior knowledge

• used to classify future observations

• cluster analysis one form