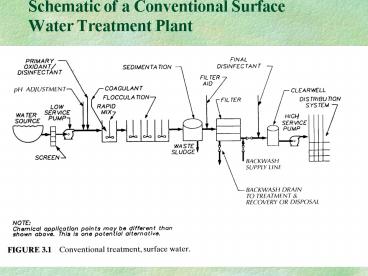
Schematic of a Conventional Surface Water Treatment Plant

1
Schematic of a Conventional Surface Water
Treatment Plant
2
Filtration Processes

• Filtration is used to remove
• 1) Suspended particulate material such as small
  flocs or precipitant particles not removed in the
  settling of coagulated or softened waters.
• 2) Turbidity-removal process such as direct
  filtration of a raw water.
• 3) Pathogenic organisms such as Giardia Lamblia
  and Cryptosporidium. (3 - 10 ?m)

3
Filtration Processes

• Types of filtration operations used in water
  treatment are
• 1) Pressure Filtration
• Expensive, Primary use in wastewater and
  industrial wastewater treatment,
• Small Systems Q typically 2 to 4 gpm/ft2.
• 2) Gravity Filtration Type
• a) High Rate (2-10 gpm/ft2) or rapid sand
  filtration usually operates in the declining rate
  mode of operation, the most widely filtration
  process in water treatment.
• b) Low Rate (0.05 gpm/ft2) or slow sand filters
  used mainly in Germany for groundwater recharge
  but also used in some small communities where a
  low turbidity surface water is used.

4
Filtration Processes
Typical Pressure Filter
5
Filtration Processes
Typical Gravity Filter
6
Filtration Processes
Gravity filtration rates will decline with time
as illustrated below
7
Filtration Process

• Backwashing
• Typically 50 bed expansion during backwashing
• Water Backwash Rate 15 - 30 gpm/ft2
• Air Backwash Rate 80 - 100 m/hr
• Backwash Cycle Time 10 - 30 minutes

8
Filtration Process

• Rapid Sand Filtration
• Sand Only 0.3-0.8 mm in diameter (Effective
  size, d10)
• 24-32 inches deep
• uniformity coefficient ? (1.4-1.8) d60/d10
• void fraction of bed, ? 0.4
• Multimedia (Anthracite and Sand)
• Coal 0.8-2 mm diameter,
• ? 0.5 void fraction of bed
• uniformity coefficient ? 1.4-1.8
• ?coal 1.4
• Sand 0.3-0.8 mm diameter, ? 0.4
• uniformity coefficient ? 1.4-1.8
• ? ? 2.6
• Depths coal--8-24 inches
• sand--10-24 inches

9
Filtration Process

• Typical Sieve Analysis of Two Filter Media

10
Filtration Process

• Example Grain Size Distribution

11
Filtration Process

• d10 is the sieve size that 10 of the total
  weight of the sample is passing.

12
Filtration Process

• Problem With Backwashing

Problem
Solution
13
Filtration Process

• DEEP FILTRATION MECHANISMS
• Calculation of the particle size which will just
  fit through the media

For DP 1 ?m Dm 6.49x10-4 cm For DP 100
?m Dm 6.49x10-2 cm
Rm (Rm RP) 0.866 RP 0.154 Rm DP 0.154 Dm
14
Filter Hydraulics

• For design purposes it is important to describe
  the headloss through porous filters. In gravity
  filtration, the driving force is the head of
  water above the filter that overcomes the
  headloss through the filter which enables
  filtration of water. The headloss is a function
  of the following variables

15
Filter Hydraulics

• In water treatment, gravity filtration is the
  normal mode of filter operation.
• Clean Filter Headloss 1.5 to 2.5 ft.
• Backwash Occurs when Hf 8 - 10 ft.
• The Carmen- Kozeny Equation describes the
  headloss in granular filters.

16
Filter Hydraulics

• The following expression can be used to calculate
  the headloss through a clean filter media

1
Carmen-Kozeny Equation
17
Filter Hydraulics

• Friction Factor Correlation

2
3
18
Filter Hydraulics
The Carmen-Kozeny equation and NR includes a
correction factor for granular materials which
are not spherical. The term is called particle
sphericity, ?.

• ? 1.0 for spherical particles
• 0.73 for pulverized coal angular sand
• 0.95 Ottawa sand
• 0.82 for rounded sand

19
Filter Hydraulics

• Now that we have developed a headloss expression
  for uniform sized filter medium in a filter bed,
  the same expression can be modified for
  non-uniform filter medium.
• The results of a sieve analysis will give the
  weight fraction between each adjacent sieve size,
  Xij. The average particle size, dij, is assumed
  to be halfway between the sieve sizes and is
  called the equivalent diameter.

di and dj are the sieve openings. This is called
the geometric mean particle size.
20
Filter Hydraulics

• The depth of the particles between adjacent sieve
  sizes can be taken as Xij L and Eq. 1 can be
  rewritten as

4
This equation assumes that the filter bed is
stratified by size and the porosity is uniform
throughout the bed.
21
Filter Hydraulics

• Notes
• Equations 1 and 4 are applicable only to clean
  filters.
• Porosity changes with time as particles
  accumulate.
• A constant filter velocity will require an
  increase in the driving force to match the
  headloss resulting from the decrease in the
  porosity.

22
Filter Hydraulics

• Notes
• In filter operation, a filter run is decreased
  when sufficient solids have deposited onto the
  filter media to
• 1) Exhaust the available driving source.
• 2) Cause the filter velocity to drop below a
  predetermined level.
• 3) Exhaust the storage capacity of the bed so
  that solids begin to appear in the effluent.
• At this point the filter must be backwashed

23
Filter Backwash Hydraulics

• Particle in Fluid

24
Filter Backwash Hydraulics

• Force balance on a collector particle being
  backwashed.

25
Filter Backwash Hydraulics
26
Filter Backwash Hydraulics
5

• where hfb head loss required to initiate
  expansion (m)
• L bed length (m)
• (1-?) fraction of packed bed occupied by the
  granular media (-)
• ?m density of the medium (Kg/m3)
• ?w density of the water (Kg/m3)

27
Filter Backwash Hydraulics
Lfb

L
?
?fb

• The headloss through the expanded bed is same as
  the headloss required to initiate expansion
  because the buoyant force of the bed is constant.

28
Filter Backwash Hydraulics

• Mass of Packed Bed Mass of Fluidized Bed

6
7
29
Filter Backwash Hydraulics

• ?fb f(terminal settling velocity of the
  particles and the backwash velocity)

The relationship between backwash velocity and
terminal settling velocity of the particles is
8
VB backwash velocity (QB/A) Vt terminal
settling velocity of the filter media
30
Filter Backwash Hydraulics

• The terminal settling velocity of the collector
  particles can be calculated based on Newtons Law
  of Settling.

31
Filter Backwash Hydraulics

• The depth of the fluidized bed and backwash
  velocity for a given medium size can be related
  as

9
This equation can be modified for a stratified
bed of non-uniform sized collector particles
10
32
Filter Backwash Hydraulics

• Assuming uniform porosity in the packed bed, Lij
  will be the depth of the layer of media
  represented by Xij. The expression of this layer
  is represented by

11
33
Filter Hydraulics

• The total expansion is the sum of the individual
  layers

12
Total expansion is usually 120 to 155 percent of
the unexpanded bed. The optimum expansion for
hydraulic backwashing occurs at expanded
porosities of 0.65 to 0.70.