k

1
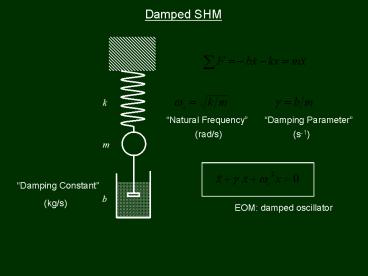
Damped SHM
k
Damping Parameter
Natural Frequency
(s-1)
(rad/s)
m
Damping Constant
b
(kg/s)
EOM damped oscillator
2
Guess a complex solution
trivial solution
Actually 2 equations
Imaginary 0
Real 0
also trivial !
3
Try a complex frequency
Real
Imaginary
A, f are free constants.
4
amplitude decays due to damping
frequency reduced due to damping
5
How damped?
Quality factor unitless ratio of natural
frequency to damping parameter
Often use it in the EOM
6
1. Under Damped or Lightly Damped
Oscillates at wo (slightly less)
Looks like SHM (constant A) over a few cycles
wo 1, g .01, Q 100, xo 1
Amplitude drops by 1/e in Q/p cycles.
7
2. Over Damped
imaginary!
part of A
Still need two constants for the 2nd order EOM
No oscillations!
8
Over Damped
wo 1, g 10, Q .1, xo 1
9
3 Critically Damped
really just one constant, and we need two. Real
solution
10
Critically Damped
wo 1, g 2, Q .5, xo 1
Fastest approach to zero with no overshoot.
11
Real oscillators lose energy due to damping.
This can be represented by a damping force in the
equation of motion, which leads to a decaying
oscillation solution. The relative size of the
resonant frequency and damping parameter define
different behaviors lightly damped, critically
damped, or over damped.