Growth of Droplets by Accretion

1
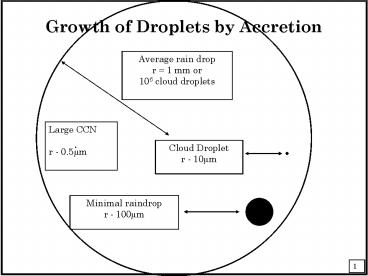
Growth of Droplets by Accretion
Average rain drop r 1 mm or 106 cloud droplets
2
Terminal Fall Speed
CD - drag coefficient Re - Reynolds number v
- droplet speed r - air density µ - dynamic
viscosity
r
When Fd Fg, drop falls relative to air at its
terminal speed.
3
Terminal Fall Speed
4
Collisions Between Drops

• Because drops of different sizes have different
  terminal speeds, larger drops overtake smaller
  ones, collide with them and perhaps coalesce to
  form larger drops.
• Collisions depend upon the relative importance of
  the inertial and aerodynamic forces and the
  separation between drop centers.
• The only important parameters affecting the
  collision of water drops in air are the ratio of
  their sizes and R3/n2, where n is the kinematic
  viscosity.

5
Collisions Between Drops
x
Mathematically, one calculates the path taken by
the droplet that allows it to make grazing
contact with the surface of the drop and
determine the original distance x within which a
collision will occur.
6
Collision Efficiency

• The effective cross-section of the drop for
  making collisions with the smaller droplet is px2
  and the ratio of this to the geometrical cross
  section is defined as the collision efficiency E

E is a function of the ratio of radii and
gR3/n2, where n is the kinematic viscosity
7
Collision Efficiency
E is small for small values of r/R for all
R E generally increases with R and r, but for
R gt 100µm, E depends largely on r. For R lt 20
µm, E is generally too small for collisions to
occur (although not 0).
Fig. 8.2 from Rogers (1989)
8
Coalescence Efficiency

• For two colliding droplets to coalesce
• air must be pushed out so that the water surfaces
  come into contact
• water surface structure must be destroyed over
  the area of contact
• two drops must deform into a sphere

It appears that coalescence takes place readily
upon collisions for droplets from about 10 to a
few hundred microns in diameter. Drops of 1 mm
diameter and larger deform on contact and air is
trapped between the surfaces (e.g., skating of
droplets on a flat water surface).
9
Collection Efficiency

• The Collection Efficiency equals the product of
  the collision efficiency and the coalescence
  efficiency. Since most coalescence takes place in
  the size range from 10 to 300 µm, it is a good
  approximation that the coalescence efficiency is
  one. Thus the collection efficiency is
  approximately the same as the collision
  efficiency. Note that there may be some
  electrical effects in thunderstorms.

10
Collector Drop Growth Geometry

• Consider
• A drop of radius R falling with terminal speed V
• Drop R is falling through and colliding with
  smaller droplets of uniform of radii r and
  terminal speed v
• The efficiency of collection of the small
  droplets by the large drop is E.

R
r
v
V
11
Collector Drop Growth Equations

• In time dt, the volume swept out by R relative to
  the moving droplets is

dV p (R r)2 (V - v) dt
12
Collector Drop Growth Equations - cont.

• Note that we have explicitly assumed a continuous
  process and have neglected the effects of
  condensation.

13
Additional Equations

• For R gtgt r ---gt

Note V is the terminal fall speed discussed in
slide 3
14
Trajectory Determination

• R may be determined as a function of height in
  the cloud given the
• Updraft speed
• Liquid water content
• initial drop size

15
Special Cases

• Size of drop on emergence from the cloud is
  independent of liquid water content.

For Stokes drops (i.e., Vk1R2)
16
Special Cases

• Minimum size for precipitation Rmin 100µm
• depends upon average cloud liquid water content.
  The minimum thickness zmin necessary for
  precipitation should be smallest for clouds with
  the warmest base temperatures, because their
  liquid water contents should be the largest.

17
Drop Radii for Different Us

• Larger Us result in larger rain drops because
  the collection occurs over a longer path

18
Final Drop Size and wl

• The final drop size is independent of wl but
  clouds with smaller wl require larger vertical
  development for a given U.

19
Drop Size dependence on Ro

• The largest drops result from the initially
  smallest drops. However, for a given updraft, the
  smaller drops require a larger vertical
  development.

20
Statistical Growth

• Even in a well-mixed cloud, there will be local
  variations in droplet concentration (i.e., wl)
• The continuous growth equations do not account
  for this, and thus apply only to average
  conditions.
• Rain results when a few fortunate drops fall
  through regions of locally high concentrations,
  thereby having more than the average number of
  collisions early in their development (Rogers,
  1989).
• Rain is produced when only one such drop out of
  105 or 106 gets an early head start.
• Statistical effects are only important in the
  first 20 or 30 collisions, after which continuous
  growth equations may be used.

21
Rain - the Evolution of the Entire Droplet
Spectrum

• The condensation-diffusion process forms a
  distribution of droplet sizes.
• The distribution evolves by random collisions (at
  first very rare) and extends itself in the
  direction of increasing drop size (Rogers and
  Yau, 1989).
• Rain forms when a portion of the distribution
  grows by gravitational coalescence and can no
  longer be held aloft by the updraft.
• See pp. 138 - 139 for the stochastic coalescence
  equation.

22
Droplet Spectrum Development by Stochastic
Coalescence
The initial unimodal distribution evolves by
coalescence into a bimodal distribution.
23
Spectrum DevelopmentEffects of Different
Processes

• Iniitial distribution consists of two modes
• S1 centered at 10 µm with wl 0.8 g m-3
• S2 centered at 20 µm with wl 0.2 g m-3
• Results shown for four different assumptions
• (a) collisions between all droplet pairs
• (b) collisions permitted only for drops in S1
• (c) collsions only between drops in S1 and S2
• (d) collisions permitted only for drops in S2

24
Spectrum DevelopmentAll droplets interact (a)
Fig. 8.11a. From Rogers and Yau (1989)

• (a) Collisions between all droplet pairs. The
  spectrum S1 is depleted and its mode value does
  not increase much from the initial value.

25
Spectrum Development (b) Autoconversion-least
efficient
Fig. 8.11b. From Rogers and Yau (1989)

• (b) Collisions are only allowed for droplets in
  S1. S2 gains only through the interaction of
  droplets in S1 and the effect is small.

26
Spectrum Development(c)Accretion - main
mechanism for water transferring from S1 to S2
Fig. 8.11c. From Rogers and Yau (1989)

• (c) Collisions occur only between drops in S1 and
  S2. The rate of transfer of water to S2 is more
  rapid than in (b) showing that accretion is more
  efficient than auto-conversion in transfering
  water from small to large drops (Rogers and Yau,
  1989).

27
Spectrum Development(d)Large hydrometeor
self-interactionMain mechanism for producing
large droplets
Fig. 8.11b. From Rogers and Yau (1989)

• (d) Collisions are permitted only for drops in
  S2. This figure shows that interactions between
  large drops flatten the tail and entend S2 to
  larger sizes.

28
Condensation Effects on Accretion

• From Rogers and Yau (1989)

29
Summary

• General Conditions Necessary for the Formation
  of Rain (Warm Rain)
• Source of Moisture
• Condensation nuclei
• Updraft to bring nuclei laden air to saturation
• Form several large droplets of radii 20 µm by
  condensation
• Continued updraft so that the drops can grow by
  collision and coalescence to radii of at least
  100 µm so that they can fall against the updraft
  and through a few hundred meters of unsaturated
  air to reach the ground.

30
Homework 2Due Oct. 23

• Problem 8.1 an 8.4 in the textbook
• Write an essay about the formation of cloud
  droplets and how they evolve into rain drops.