Ways that well cover to compare two means'

1
(No Transcript)
2
Ways (that well cover) to compare two means.

• Assuming variances are known
• Variances are unknown but assumed to be equal
• Variances are unknown and not assumed to be equal
• The samples are paired

3
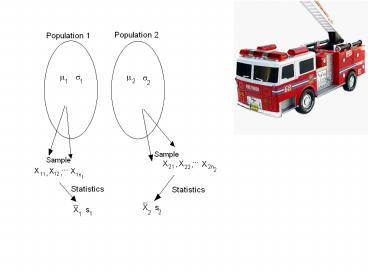
0. Name populations
1. H0 m1 m2 0, H1 m1 m2 0
2. Zobs N(0,1) if H0 is true
3. za (left tailed), z1-a (right tailed) , za/2 ,
z1-a/2 (two tailed)
4. Reject H0 if Zobs lt za (left tailed)
Reject H0 if Zobs gt z1-a (right tailed)
Reject H0 if Zobs lt za/2 or Zobs gt z1-a/2
5. Compute test statistic
6. Reject H0 or Fail to reject H0 7. Form
conclusion
4
0. Name populations
1. H0 m1 m2 0, H1 m1 m2 0
2. Zobs N(0,1) if H0 is true
3. Reject H0 if p-value lt a
4. Compute test statistic
5. P(Z lt Zobs) (left tailed) P(ZgtZobs) (right
tailed) P(Zlt-Zobs or ZgtZobs) (two tailed)
6. Reject H0 or Fail to reject H0 7. Form
conclusion
5
Point estimate
Margin of error
Standard error of the point estimate
6
The U.S. National Center for Health Statistics
compiles on the length of stay by patients in
short term hospitals. Independent samples of 19
males and 15 females were obtained and the
average length of stay was found to be 8.48 days
for males and 7.11 days for females. Assume the
standard deviations for males and females are 5.4
and 4.6 days respectively. With 95 confidence,
test for a difference between the means of these
populations.
Pop 1 males Pop 2 females x1 8.48 x2
7.11 s1 5.4 s2 4.6 n1 19 n2 15 1 a
0.95 Test for a difference between the means
7
0. Pop 1 males, Pop 2 females
1. H0 m1 m2 0, H1 m1 m2 0
2. Zobs N(0,1) if H0 is true
3. z0.025 -1.96, z0.975 1.96
4. Reject H0 if Zobs lt -1.96 or Zobs gt 1.96
5. Compute test statistic
6. Fail to reject H0 7. With 95 confidence there
is insufficient evidence to conclude the mean
length of hospital stay differs by sex.
8
0. Pop 1 males, Pop 2 females
1. H0 m1 m2 0, H1 m1 m2 0
2. Zobs N(0,1) if H0 is true
3. Reject H0 is p-value lt 0.05
4. Compute test statistic
5. P(Z lt -0.80 or Z gt 0.80) 0.4238 6. Fail to
reject H0 7. With 95 confidence there is
insufficient evidence to conclude the mean length
of hospital stay differs by sex.
9
With 95 the difference between the mean male and
mean female length of stay is between -1.99 and
4.73 days. Note We would interpret this as no
difference between the means since the interval
includes 0.
10
Some statistics students complain that graphing
calculators give students an advantage over
students without such calculators. To check this
contention, forty-five students were randomly
assigned to two groups twenty-three use graphing
calculators, twenty-two using standard
calculators. The students then took an exam and
the average score for the graphing calculator
group was found to be 82.7 and the average for
the standard calculator group was 77.9. Assume
the standard error for the graphing group is 1.46
and 1.66 for the standard calculator group. Test
the students contention with 90 confidence.
Pop 1 graphing calc Pop 2 standard
calc 1 a 0.90 Test for mean for pop 1
is higher than mean for pop 2
11
0. Pop 1 graphing calculator, Pop 2 standard
calculator
1. H0 m1 m2 0, H1 m1 m2 gt 0
2. Zobs N(0,1) if H0 is true
3. z0.90 1.28
4. Reject H0 if Zobs gt 1.28
5. Compute test statistic
6. Reject H0 7. With 90 confidence there is
sufficient evidence to conclude the mean score
for students using graphing calculators is higher
than the mean score obtained using a standard
calculator.
12
0. Pop 1 graphing calculator, Pop 2 standard
calculator
1. H0 m1 m2 0, H1 m1 m2 gt 0
2. Zobs N(0,1) if H0 is true
3. Reject H0 is p-value lt 0.1
4. Compute test statistic
5. P(Z gt 2.17) 0.0150 6. Reject H0 7. With 90
confidence there is sufficient evidence to
conclude the mean score for students using
graphing calculators is higher than the mean
score obtained using a standard calculator.
13
Suppose we arent willing to assume that the
variances are known. Suppose the samples are
still independent If maxs1,s2 / mins1,s2 lt 2
then we do the pooled t-test to compare the
means If its reasonable to assume that s1 s2
then we pool over the samples to get a better
estimate of the variance.
14
0. Name populations
1. H0 m1 m2 0, H1 m1 m2 0
2. tobs tdf if H0 is true (where df
n1n2-2)
3. -tdf,a (left tailed), tdf,a (right tailed) ,
-tdf,a/2, tdf,a/2 (two tailed)
4. Reject H0 if tobs lt -tdf,a (left tailed)
Reject H0 if tobs gt tdf,a (right tailed)
Reject H0 if tobs lt -tdf,a/2 or tobs gt tdf,a/2
5. Compute test statistic
6. Reject H0 or Fail to reject H0 7. Form
conclusion
15
0. Name populations
1. H0 m1 m2 0, H1 m1 m2 0
2. tobs tdf if H0 is true (where df
n1n2 2)
3. Reject H0 if p-value lt a
4. Compute test statistic
5. p-value use a computer
6. Reject H0 or Fail to reject H0 7. Form
conclusion
16
(No Transcript)
17
Previous research indicates children borne by
diabetic mothers may suffer from high blood
pressure. Random samples of adolescent offspring
of diabetic mothers (ODM) and non-diabetic
mothers (ONM) were taken and systolic blood
pressure was measured. Of the 24 ODM offspring,
the average systolic blood pressure was 118 mm Hg
with a standard deviation of 12.04 mm Hg. In the
ONM sample of 18, the average systolic blood
pressure was 110 mm Hg with a standard deviation
of 11.25 mm Hg. Test the conjecture with 99
confidence.
Pop 1 ODM Pop 2 ONM 1 a 0.99 Test
if mean for ODM is higher than mean for ONM
18
0. Pop 1ODM, Pop 2ONM
1. H0 m1 m2 0, H1 m1 m2 gt 0
2. tobs t40 if H0 is true
3. t40,0.005 2.704
4. Reject H0 if tobs gt 2.704
5. Compute test statistic
6. Fail to reject H0 7. With 99 confidence there
is insufficient evidence to conclude that the
mean blood pressure level in the diabetic
population is higher than the non-diabetic
population.
19
0. Pop 1ODM, Pop 2ONM
1. H0 m1 m2 0, H1 m1 m2 gt 0
2. tobs t40 if H0 is true
3. Reject H0 if p-value lt 0.01
4. Compute test statistic
5. p-value 0.0172 6. Fail to reject H0 7. With
99 confidence there is insufficient evidence to
conclude that the mean blood pressure level in
the diabetic population is higher than the
non-diabetic population.
20
Time for change SAS
21
Suppose we arent willing to assume that the
variances are known. Suppose the samples are
still independent If maxs1,s2 / mins1,s2 gt 2
then we do the separate variance t-test to
compare the means If its reasonable to assume
that s1 s2 then we pool over the samples to get
a better estimate of the variance.