Quantization

1
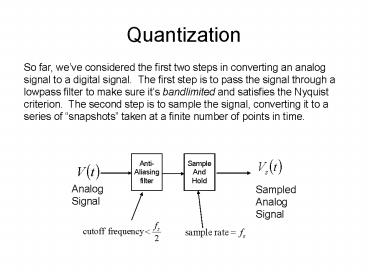
Quantization
So far, weve considered the first two steps in
converting an analog signal to a digital signal.
The first step is to pass the signal through a
lowpass filter to make sure its bandlimited and
satisfies the Nyquist criterion. The second step
is to sample the signal, converting it to a
series of snapshots taken at a finite number of
points in time.
Sample And Hold
Anti- Aliasing filter
Analog Signal
Sampled Analog Signal
2
Quantization
After sampling, the signal exists as a series of
snapshots, or samples. Each of these samples
for an example signal (a 1 kHz sine wave sampled
at 22 kHz) is represented by a small circle in
the plot at left. Ideally, the Voltage of each
sample is exactly the signal Voltage at the time
the sample is taken. Notice that there are 22
samples taken per millisecond.
3
Quantization
After sampling, the signal exists as a series of
samples, without the line between samples. There
are a finite number of samples for any
finite-length interval of time, but each of the
samples still has an infinite number of possible
values. These sample values cannot be
represented by integers, as they must be to be
processed by a digital system. The third step is
to convert them to values which can be
represented by integers. This is called
quantization.
4
Quantization
The sample and hold circuit is followed by a
quantizer, which chooses one of a finite set of
integers to represent each of the samples.
Sample And Hold
Anti- Aliasing filter
N-bit quantizer
Sampled Analog Signal
Analog Signal
5
Quantization
The simplest way to quantize this series of
samples is to use a single bit to represent each
sample. If V (nT) lt 0, then Vq(n) 0 otherwise
Vq(n) 1. Unfortunately, a sine wave quantized
in this manner would be indistinguishable from a
sawtooth, triangle or square wave. The sample
Voltages (before quantization are represented by
the blue circles, the corresponding quantized
values (0 or 1) are represented by the red
circles.
6
Quantization
Each quantized sample constitutes an estimate of
the sample Voltage (and of the signal Voltage).
This Voltage estimate is represented by Vq in the
plot at left. Obviously, this is not a very good
estimate.
7
Quantization
If we were to recover the signal from this
sequence of quantized samples, we would recover a
square wave with an amplitude of 1 Volt. Each of
the quantized samples has an associated error
Voltage Ve
Vq represents Voltage estimated by the quantizer,
V represents the signal Voltage, and Ve
represents the error.
8
Quantization
Here, the signal Voltage is shown in blue and the
error Voltage is shown in red. How can the error
Voltage be reduced? Theres only one way. We
have to divide the input range (-1 Volt to 1
Volt in this example) into a larger number of
segments. If we use 2-bit integers to represent
each sample, we can double the number of possible
values for our estimate of the input Voltage.
This doubles the resolution of the quantizer, and
cuts the quantization error in half.
9
Quantization
Heres what we get when we quantize the same
signal to 2-bit resolution. The quantizer output
has 4 possible values, and must be signed because
of the bipolar (both positive and negative) input
range. If twos complement integers are used,
the quantizer output isnt symmetrical - Its
maximum positive value is only 1, but its maximum
negative value is -2.
10
Quantization
Notice that the maximum error voltage is reduced
by half, compared with the error Voltage of a one
bit quantizer.
11
Quantization
Using 3-bit integers doubles the number of
segments the input range is divided into to 8,
doubling the resolution again ...
12
Quantization
and this cuts the error Voltage in half again.
13
Quantization
Every time we add a bit to the word length, we
double the resolution
14
Quantization
And cut the error Voltage in half. The result of
4-bit quantization is shown here. 8-bit
resolution is considered low resolution.
CD-quality audio means 16-bit resolution.
15
Quantization
This sine wave is a deterministic (i.e.,
predictable) signal. Once its been identified,
it carries no useful information (tells us
nothing we didnt know) unless something about it
(e.g., frequency, amplitude, phase, or shape)
changes. All useful signals are, from the
receivers viewpoint, random processes. A
deterministic signal is worthless.
16
Quantization
When a deterministic signal like this sine wave
is quantized, the error Voltage is also
deterministic. When a random process like speech
or music, or data transmission, is quantized, the
error is also a random process. We have a name
for random errors Noise!
17
Quantization
The quantization error Voltage is equivalent to a
noise Voltage at the input to the quantizer.
N-bit quantizer
S
V(nT)
Sampled Analog Signal
Ve(nT)
Equivalent Quantization Noise
18
Quantization
The maximum signal amplitude is fixed for a given
input Voltage range, so the maximum signal power
is fixed. The noise power can be reduced, and
therefore the maximum signal to noise ratio
increased, by simply adding bits to the word
length. This is one of the beautiful things
about digital signal processing.
19
Quantization
The ratio of the maximum signal power to the
average noise power, expressed in decibels, is
called the dynamic range. Ideally, wed like the
quantization noise to be the dominant source of
noise in the system. This means the
input-referred noise of the sampler, the DAC, and
all other parts of the system make a smaller
contribution to the total output noise than the
quantizer. The quantization noise is
controllable.
20
Quantization
Lets find out what the dynamic range is for an
N-bit quantizer If the quantizers input Voltage
range spans Vp Volts to Vp Volts (Vp 1 Volt
in this example), and if the signal is a
full-scale sinusoid (occupies the entire
quantizer input Voltage range), then the input
signal is described by
The RMS signal Voltage is
The signal power, on a 1-Ohm basis, is
21
Quantization
Now we have to find the power of the quantization
noise. An N-bit quantizers input range (-Vp to
Vp), a 2 Vp range of input Voltages, is divided
into 2N
segments, each of which spans a Voltage range of

D represents the change in input Voltage which
results in a 1-LSB (least significant bit) change
in quantizer output. Well model the
quantization noise as a random variable,
uniformly distributed over the Voltage range
22
Quantization
Next, we find the mean-squared value of the
quantization noise Voltage, which (on a 1-Ohm
basis) is equal to the quantization noise power
So for an N-bit quantizer with a sinusoidal
input, the greatest possible signal-to-noise
ratio (which is equivalent to the dynamic range
is
23
Quantization
So
24
Quantization
Expressing the maximum SNR in decibels,
25
Quantization
The quantizers maximum SNR is equal dynamic
range, so
Notice that increasing the word length, N, by 1
increases the dynamic range by 6 dB. The dynamic
ranges of several common word lengths are given
below
26
Quantization
For purposes of comparison, the dynamic range of
magnetic tape is 55 dB. The theoretical maximum
dynamic range that can be recorded on an old-
style vinyl phonograph record is approximately
110 dB (based on the size of the vinyl
molecules), but the best that can be reproduced
using a high-quality phonograph cartridge and
stylus is about 60 dB. CD quality audio has 16
bit dynamic range. The maximum SNR (or dynamic
range) of the quantizer doesnt necessarily tell
the whole story, because it doesnt exist by
itself.
27
Quantization
The front end of a digital signal processing
system, the part of the system that converts an
analog signal to a digital signal, consists of
several stages an anti-aliasing filter, a
sample-and-hold circuit, and the quantizer.
Sample And Hold
Anti- Aliasing filter
N-bit quantizer
28
Quantization
Each of these has its own input-referred noise
variance (power), which contribute to the overall
system noise.
Sample And Hold
Anti- Aliasing filter
N-bit quantizer
S
S
S
Input-referred noise of sample and hold
Quantization noise
Input-referred noise of filter
29
Quantization
There may also be one or more stages of
amplification preceding the anti-aliasing filter.
This also contributes noise.
Sample And Hold
Anti- Aliasing filter
N-bit quantizer
A
S
S
S
S
Input-referred noise of sample and hold
Quantization noise
Input-referred noise of filter
Input-referred noise of amplifier
30
Quantization
Each of these noise contributions, including the
quantization noise, may be referred to the system
input. That is, each may be replaced by a noise
source of the correct noise variance (power) at
the system input.
N-bit quantizer
Sample And Hold
Anti- Aliasing filter
A
S
Input-referred noise of amplifier
Input noise of filter, referred to system input
Quantization noise referred to system input
Input noise of sample and hold, referred to sytem
input
31
Quantization
Each of these noise contributions, including the
quantization noise, may be referred to the system
input. That is, each may be replaced by a noise
source of the correct noise variance (power) at
the system input.
N-bit quantizer
Sample And Hold
Anti- Aliasing filter
A
S
Input-referred noise of amplifier
Input noise of filter, referred to system input
Quantization noise referred to system input
Input noise of sample and hold, referred to sytem
input
32
Quantization
Were interested in comparing the effect of
quantization noise to the total effect of all
other noise sources, so well combine the noise
of the amplifier, filter, and sample-and-hold
into a single noise source, Na (analog noise).
Well call the quantization noise Nq.
N-bit quantizer
Sample And Hold
Anti- Aliasing filter
A
S
Na
Now, the maximum signal-to-noise ratio is
Nq
33
Quantization
If Na is greater than Nq, and enough greater to
be the dominant noise source,
Sample And Hold
Anti- Aliasing filter
N-bit quantizer
A
S
Na
Next, measure the output SNR. Convert this to an
equivalent word length by solving
Nq
For N
This gives us the word length for an ideal
quantizer, preceded by a noise-free amplifier,
filter, and sample-and-hold, which would give the
same maximum SNR. This is the effective word
length, or Effective Number of Bits (ENOB) of the
system.
34
Quantization
For example, consider a 12-bit analog-to-digital
converter (ADC). It includes a sample-and-hold,
but is preceded by a filter and an amplifier.
Sample And Hold
Anti- Aliasing filter
N-bit quantizer
A
S
Na
Suppose the output signal-to-noise ratio is 61
dB. Calling the ENOB Neff,
Nq
Of course, we cant have a word length of 9.84
bits, we have to use 10. This means that we
could use a (cheaper) 10 bit ADC instead of a 12
bit ADC with no degradation of system performance.