Chapter 10: Capital Budgeting

1
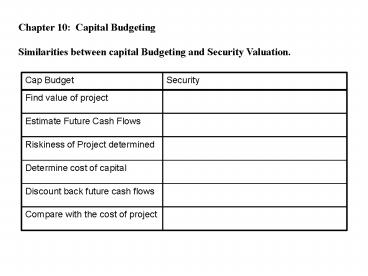
Chapter 10 Capital Budgeting   Similarities
between capital Budgeting and Security Valuation.
2

• Capital Budgeting decision rules
• 1. Pay-back period.
•  
• 2. Discounted Pay-back period.
•  
• 3. NPV (net present value)
• 4. IRR (internal rate of return)
• 5 MIRR (modified internal rate of return)

3

• Capital Budgeting decision rules
• Pay-back period
•  
• A. How many years does it take for our firm to
  recoup our initial cash flow (initial cost of
  project)??
•  
• B. Calculated by adding projects cash inflows
  to its cost until the cumulative cash flow for
  the project turns positive.
•  
•  

4
Payback Period example  
5

• Pay back period
• Problems
•  
• Strengths
• - Easy to calculate and understand.
•  
• Weaknesses
• - Ignores the time value of money.
• - Ignores CFs occurring after the payback
  period.
•  
•  

6

• Discounted Pay back
• - Uses discounted cash flows rather than raw
  CFs.
• - Assume that the WACC 10
•  

7

• NPV (Net Present Value)
• - Sum of the PVs of all cash inflows and
  outflows of a project 

8

• NPV continued  

9

• Solving for NPV Financial calculator solution
•  
• Enter CFs into the calculators CFLO register.
• - CF0 -600
• - CF1 200
• - CF2 200
• - CF3 200
• - CF4 600
• - CF5 600
• - CF6 600
•  
• Enter I/YR 10, press NPV button to get NPV1
  1,018
•  

10

• Rationale for the NPV rule
•  
•  
•  
• If projects are independent, accept if
•  
•  
•  
• If projects are mutually exclusive, accept
•  
•  
•  
• In this example, would accept project 2 if
  mutually exclusive (NPV2 gt NPV1), and would
  accept both if independent.
•  
•  

11

• IRR Internal Rate of Return
• - IRR is the discount rate that forces PV of
  inflows equal to cost, and the NPV 0
•  
•  
•  
•  
•  
•  
• How is a projects IRR similar to a bonds YTM?
• - EXAMPLE Suppose a 10-year bond with a 9
  annual coupon sells for 1,134.20.
• Solve for IRR YTM 7.08, the annual return
  for this project/bond.
• PV -1134.20
• PMT 90
• FV 1000
• N 10
• I ??

12

• EXAMPLE (contd) Suppose a 10-year bond with a
  9 annual coupon sells for 1,134.20.
•  
• - CFo -1134.20
• - CF1 90
• - CF2 90
• - CF3 90
• - CF4 90
• - CF5 90
• - CF6 90
• - CF7 90
• - CF8 90
• - CF9 90
• - CF10 1090
• - IRR ??
•  

13
IRR (contd) 
14
IRR (contd)   If IRR gt Cost of Capital,
then     If IRR lt Cost of Capital, then     If
IRR gt WACC, the projects rate of return is
greater than its costs. There is some return
left over to boost stockholders returns.     It
is the projects expected rate of return.     Ease
of comparison between cost of capital and IRR.  
15
IRR (contd) acceptance criteria  

• If projects are independent
• If projects are mutually exclusive

16
NPV profiles Why use? 
17

• Potential Problem with IRR Method
• Multiple IRRs

• At very low discount rates, the PV of CF7 is
  large negative, so NPV lt 0.
• At very high discount rates, the PV of both
  CF1-CF7 are low, so CF0 dominates and again NPV lt
  0.
• In between, the discount rate hits CF7 harder
  than CF1-CF4, so NPV gt 0.
• Result 2 IRRs.

18
Multiple IRRs 
19

• Reinvestment rate assumptions
•  
•   
• NPV method assumes CFs are reinvested at
•  
• IRR method assumes CFs are reinvested at
•  
• NPV method should be used to choose between
  mutually exclusive projects.
•  
• Perhaps a hybrid of the IRR that assumes cost of
  capital reinvestment is needed.
•  

20

• Modified Internal Rate of Return
•  
• MIRR is the discount rate that causes the PV of a
  projects future value (FV) to equal the PV of
  costs. FV is found by compounding inflows at
  WACC.
•  
• MIRR correctly assumes reinvestment at
•  
• MIRR also avoids
•  
• Managers like rate of return comparisons, and
  MIRR is better for this than IRR.

21
(No Transcript)
22
(No Transcript)