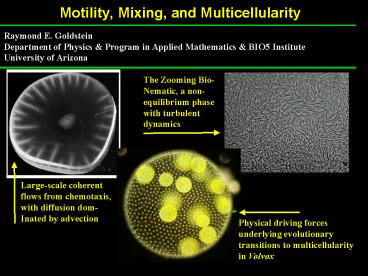
Motility, Mixing, and Multicellularity

1
Motility, Mixing, and Multicellularity
Raymond E. Goldstein Department of Physics
Program in Applied Mathematics BIO5
Institute University of Arizona
The Zooming Bio- Nematic, a non- equilibrium
phase with turbulent dynamics
Large-scale coherent flows from chemotaxis, with
diffusion dom- Inated by advection
Physical driving forces underlying evolutionary
transitions to multicellularity in Volvox
2
Bacterial Swimming and Chemotaxis
Macnab and Ornstein, J. Mol. Biol. (1977)
Real-time Imaging of Fluorescent Flagella
1-4 mm
10-20 mm
Turner, Ryu, and Berg, J. Bacteriol. (2000)
20 nm
normal LH helix curly RH helix straight
straight
Swimming speed 10 mm/s Propulsive force 1 pN
3
Advection, Dissipation Diffusion Reynolds and
Peclet Numbers
Navier-Stokes equations
Passive scalar dynamics
Reynolds number
Peclet number
If U10 mm/s, L10 mm, Re 10-4, Pe 10-1 At
the scale of an individual bacterium, dissipation
dominates inertia, and advection dominates
diffusion. The second relation breaks down with
multicellularity
4
Part I. Bacterial Self-Concentration
1 cm
Dombrowski, Cisneros, Chatkaew, Goldstein
Kessler, Self-concentration and large-scale
coherence in bacterial dynamics, PRL 93, 098103
(2004)
Tuval, Cisneros, Dombrowski, Wolgemuth, Kessler
Goldstein, Bacterial swimming and oxygen
transport near contact lines, PNAS 102, 2277
(2005)
5
Mechanism of Self-Concentration
Dombrowski, et al. (2004)
6
The Boycott Effect (in Sedimentation)
g
A.E. Boycott, Nature 102, 532 (1920). A.A.
Acrivos and E. Herbolzheimer, J. Fluid Mech. 92,
435 (1979).
7
Side Views Depletion and Flow
2 mm
Video 100x actual speed
Dombrowski, et al. (2004)
8
Diffusion and Chemotaxis
Oxygen diffusion/advection
Chemotaxis
Navier-Stokes/Boussinesq
depletion layer D/v
n(z)
C(z)
z
z
9
Experiment vs. Theory
Tuval, et al. PNAS (2005)
10
Moffat Vortex
1 mm
Experiment (PIV)
Numerics (FEM)
Tuval, et al. (2005)
11
Chemotactic Singularities Mixing
Stirring re-oxygenates the entire drop
Tuval, et al. (2005)
12
Part II. The Zooming Bio-Nematic Phase
contact line
Petri dish
300 mm
Dombrowski, Cisneros, Chatkaew, Goldstein
Kessler, Self-concentration and large-scale
coherence in bacterial dynamics, PRL 93, 098103
(2004)
13
Velocity Field from PIV (pendant drop)
Peclet number 10-100 (vs. 0.01-0.1 for
individual bacterium)
35 mm
Dombrowski, et al. (2003). See also Wu and
Libchaber (2000)
14
Velocity Correlation Functions in Space Time
space
oscillations due to multiple vortices (individual
images)
sequence average
time
oscillations due to recurring vortices (individual
images)
spatial average
15
Advection of Microspheres
contact line
16
Historical Ideas

• Flocking models (Toner and Tu, 1995, traffic
  flow)

A Landau theory in the velocity field clever
but not at all faithful to the physics of Stokes
flow

• Sedimentation (interacting Stokeslets)

as few as three particles exhibit
chaotic trajectories (Janosi, et al., 1997)

• Conventional chemotaxis picture (e.g.
  Keller-Segel) - MISSES ADVECTION

Velocity field must be determined
self-consistently with density field

• A synthesis is emerging from coarse-grained
  models of sedimentation
• (Bruinsma, et al.) and of self-propelled
  objects (Ramaswamy, et al.)

IMPLICATIONS FOR QUORUM SENSING
17
(consider the Volvocalean green algae)
Part III. Driving Forces for Multicellularity
Chlamydomonas
V. carteri
Discovered by van Leeuwenhoek (1700), name means
fierce roller
18
The Diffusional Bottleneck
Smoluchowski result diffusion to an
absorbing sphere
Number of peripheral cells, and hence
their requirements, scale as R2
Fluxes
Organism radius R
19
Volvox On A Stick
S. Ganguly
Solari, Ganguly, Kessler, Michod Goldstein,
Multicellularity and the Functional
Interdependence Of Motility and Molecular
Transport, preprint (2005).
20
Stirring by Volvox carteri
21
A Closer View
22
Even Closer (Flagellar Motions Visible)
23
Locally Chaotic Advection
24
High-Speed Movie (125 fps) of Volvox Flagella
25
Flow Field Viewed On Axis
26
Fluid Velocities During Life Cycle

• Hatch
• Division
• Daughter
• Pre-Hatch

Solari, et al. (2005)
27
Peclet Number During Life Cycle (Large!)
Solari, et al. (2005)
28
Flagellar-Driven Flows and Scaling Laws
Specified shear stress t at surface
Detailed calculation (Gegenbauer polynomials,
etc.) yields
This implies that the Peclet number scales as
Finally, large Pe scaling (FluxRPe1/3) yields
This almost eliminates the bottleneck!
29
Velocity Profile
Solari, et al. (2005a)
30
Issues
Transport, mixing, and chemical signaling at
high concentrations quorum sensing, etc.
(biology, nonequilibrium statistical mechanics,
) Mixing, metabolism, and evolutionary
transitions to multicellularity germ-soma
differentiation, vascularization, morphological
transformations