Cubic Polynomial PowerPoint PPT Presentations
All Time
Recommended
Chapter 6 Polynomials and Polynomial Functions
| PowerPoint PPT presentation | free to view
Standard form: terms arranged in descending order by degree ... x2 2 xy y2 -b2. Polynomials with quadratic coefficient other than 1 (2x2 - 7x -15) ...
| PowerPoint PPT presentation | free to view
0 and 3 are double roots 3 roots; x = 2, 2, 2 Double roots Double roots (tangent) Triple root lies flat then crosses axis (wiggles) Given Roots, ...
| PowerPoint PPT presentation | free to view
Division and Rational Root Theorem TS: Making decisions after reflection and review Obj: Review polynomial division and how to find the roots of polynomials
| PowerPoint PPT presentation | free to download
Write the polynomials in standard form and identify the polynomial by degree and number of terms. 1. 2. This is a 3rd degree, or cubic, trinomial.
| PowerPoint PPT presentation | free to view
Be able to determine the degree of a polynomial. Be able to classify a polynomial. Be able to write a polynomial in standard form. Monomial: A number, a variable or ...
| PowerPoint PPT presentation | free to download
Polynomials have no variables in denominators or exponents, no roots or absolute values of variables, and all variables have whole number exponents.
| PowerPoint PPT presentation | free to download
Instead of using pow(x,k), or any iterative/recursive subroutines, think again! ... Original quintic. Converged to 3. in many steps (5 was not a good guess for 3) 18 ...
| PowerPoint PPT presentation | free to view
Polynomial Functions
| PowerPoint PPT presentation | free to download
CLASSIFYING POLYNOMIALS by: GLORIA KENT Degree of a Polynomial (Each degree has a special name ) Degree of a Polynomial (Each degree has a special name ...
| PowerPoint PPT presentation | free to view
Each term is the product of a real-number coefficient and a ... Use synthetic substitution to show that f(x) = 3x3 x2 19x 10 has only one integral zero. ...
| PowerPoint PPT presentation | free to view
Chapter 6 Polynomial Equations Algebra Linear Equations and Eliminations Quadratic Equations Quadratic Irrationals The Solution of the Cubic Angle Division
| PowerPoint PPT presentation | free to download
POLYNOMIALS REVIEW The DEGREE of a polynomial is the largest degree of any single term in the polynomial (Polynomials are often written in descending order of the ...
| PowerPoint PPT presentation | free to download
Factorising polynomials This PowerPoint presentation demonstrates three methods of factorising a polynomial when you know one linear factor. Click here to see ...
| PowerPoint PPT presentation | free to download
Operations with polynomials Polynomials A polynomial in x is an expression of the form where a, b, c, are constant coefficients and n is a nonnegative integer.
| PowerPoint PPT presentation | free to download
UNIT 3 POLYNOMIALS 5-1 Graphing Polynomials Key Terms for Classifying Polynomials Define: Polynomial is a monomial or a sum/difference of monomials.
| PowerPoint PPT presentation | free to view
Polynomial and Synthetic Division #3 Common Core objectives: * Students will be able to use long division to divide polynomials by other polynomials.
| PowerPoint PPT presentation | free to download
Section 5.4 Dividing Polynomials Review of Long Division What terms do we use to describe 672 and 21? Because the reminder is zero, we know that 21 is a factor of 672.
| PowerPoint PPT presentation | free to download
The coefficient of x3 gives the steepness' of the curve. y = x3. y = -x3. Negative coefficients of x3 gives curves the other way round. The Cubic Function : y = (x-k)3 ...
| PowerPoint PPT presentation | free to view
Taylor Polynomial Approximations A graphical demonstration Best first order (linear) approximation at x=0. OZ calls this straight line function P1(x).
| PowerPoint PPT presentation | free to download
Multiplying Polynomials: You can multiply polynomials vertically, just like you would in an ordinary arithmetic problem. The same pattern works with polynomials.
| PowerPoint PPT presentation | free to download
The 'degree of the polynomial' is the same as the degree of the term with the highest degree. ... A polynomial with one term is called a monomial. ...
| PowerPoint PPT presentation | free to view
Polynomial and Synthetic Division Pre-Calculus Mrs.Volynskaya The Remainder and Factor Theorems The remainder obtained in the synthetic division process has an ...
| PowerPoint PPT presentation | free to view
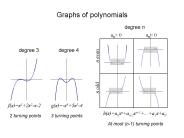
6.2 Graphs of Polynomials The Degree of Polynomials The Leading Coefficient of a Polynomial End Behavior of Polynomials End Behavior of Polynomials End Behavior of ...
| PowerPoint PPT presentation | free to view
Polynomials of High Degree As the degree of a polynomial function increase it becomes more difficult to create and accurate graph but here are some hints that will ...
| PowerPoint PPT presentation | free to view
Henrik John Andersen/Ole Madsen. With Via Point. User Specifies Velocity in Via Points ... Henrik John Andersen/Ole Madsen. Linear Function with Parabolic ...
| PowerPoint PPT presentation | free to view
... the sum of its height and the perimeter of the base is not more than 72 inches. ... Two congruent squares are removed from one end of a rectangular 10-inch by 20 ...
| PowerPoint PPT presentation | free to view
Polynomial Functions and Their Graphs
| PowerPoint PPT presentation | free to download
... Early Polynomials Arab and Indian Mathematicians Dominated during period between Greek ... An extension K/k is a radical extension if there is a tower of ...
| PowerPoint PPT presentation | free to download
When you zoom out, the effect of the lower degree terms is difficult to see. f(x)=x3 2x2-x-2 ... Thus a zero of this function must lie between -5 and 5. ...
| PowerPoint PPT presentation | free to download
Solving Polynomial Equations by Graphing Types of Equations Quadratic - has the form ax2 + bx + c = 0 Highest exponent is two (this is the degree) The most real ...
| PowerPoint PPT presentation | free to download
There exists a unique polynomial of degree at most n, , that satisfies ... Runge's phenomenon. ... the Bernstein polynomial converges to the Runge's function on [-1,1] ...
| PowerPoint PPT presentation | free to download
Now multiply 2x by x 2. and subtract. Algebraic long division. Bring down the next term, -x. ... x multiplied by ax gives ax . so a must be 2. Dividing in ...
| PowerPoint PPT presentation | free to view
7.5 Zeros of Polynomial Functions Objectives: Use the Rational Root Theorem and the Complex Conjugate Root Theorem. Use the Fundamental Theorem to write a polynomial ...
| PowerPoint PPT presentation | free to view
7.1 An Introduction to Polynomials Objectives: Identify, evaluate, add, and subtract polynomials. Classify polynomials, and describe the shapes of their graphs.
| PowerPoint PPT presentation | free to view
How to use transformations to sketch graphs of Polynomial Functions ... important in modeling various aspects of nature and can be used to provide ...
| PowerPoint PPT presentation | free to view
Linear Function: f(x) = -5x 1. Quadratic Fcn: f(x) = 3x2 5x 1 ... models the ocean temperature in degrees F at Naples, FL. ...
| PowerPoint PPT presentation | free to view
Polynomial Approximation PSCI 702 October 05, 2005 What is a Polynomial? Functions of the form: Polynomial of degree n, having n+1 terms. Will take n(n+1)n/2 ...
| PowerPoint PPT presentation | free to download
Simpson's Rule on a Cubic Why is the Simpson's Rule approximation of a degree 3 polynomial exact? a b First, let's shift the function so that the interval is centered ...
| PowerPoint PPT presentation | free to download
If you find factorising by inspection difficult, you may find this method easier. ... The method you are going to see now is basically the reverse of this process. ...
| PowerPoint PPT presentation | free to view
Objectives: To divide polynomials using long and synthetic division To apply the Factor and Remainder Theorems to find real zeros of polynomial functions
| PowerPoint PPT presentation | free to download
Enter Ferrari, Cardano's student ... Ferrari's result in Ars Magna. Ferrari ... See Ferrari's listing on MACTUTOR. Quintic (fifth degree) Polynomials ...
| PowerPoint PPT presentation | free to view
Reference Link: https://myassignmenthelp.com/blog/how-to-solve-cubic-equation-step-by-step/ For Order: https://myassignmenthelp.com/Home/ Email id: contact@myassignmenthelp.com The coefficients of a, b, c and d are real or complex numbers with a not equals to zero (a ≠ 0). It must have the term x3 in it, or else it will not be a cubic equation. But any or all of b, c and d can be zero.
| PowerPoint PPT presentation | free to download
... Cardano's friend Ferrari tried to defend Cardano. 12 printed pumphlets 'Cartelli' (Ferrari vs. Cardano) This led to a public contest which was won by Ferrari ...
| PowerPoint PPT presentation | free to download
1.4 - Dividing Polynomials MCB4U (A) Review recall the steps involved in long division: set it up using the example of 30498 39 (B) Division of Polynomials by ...
| PowerPoint PPT presentation | free to view
Xi2 = math test score. But again, multicollinearity issues ... 9.92 0.167 Verbal 0.138 Math - 0.00111 VSq -0.000843 MSq 0. ... Use Calc Calculator...
| PowerPoint PPT presentation | free to view
STAT. CALC. 5: QuadReg. Polynomial Models. Polynomial Models. 7.71. 2000 ... STAT. CALC. 6: CubicReg. Polynomial Models. In-Class. 1, 2, 3, 4, 5, 6, 7, 14, 28 ...
| PowerPoint PPT presentation | free to view
Title: 6 -6 Factoring by Grouping Author: Jerry Last modified by: E200701017 Created Date: 1/28/2006 4:20:13 PM Document presentation format: On-screen Show
| PowerPoint PPT presentation | free to download
Title: 6 -6 Factoring by Grouping Author: Jerry Last modified by: PCKankolenski Created Date: 1/28/2006 4:20:13 PM Document presentation format: On-screen Show (4:3)
| PowerPoint PPT presentation | free to download
Adding and Subtracting Polynomials Module VII, Lesson 1 Algebra Online VHS@PWCS What is a polynomial? A polynomial is one term or the sum or difference of two or more ...
| PowerPoint PPT presentation | free to view
Polynomial and Rational Functions Chapter 3 TexPoint fonts used in EMF. Read the TexPoint manual before you delete this box.: AAAA Quadratic Functions and Models ...
| PowerPoint PPT presentation | free to view
Coauthors: Hao Cheng, John E. Lavery, Yong Wang, Wei ... Haptic devices design. Shape-preservation. One fundamental requirement is that splines should be ' ...
| PowerPoint PPT presentation | free to view
Polynomials and Taylor Series: How Functional is your Function ? Earth's Interior temperature profile How well would a linear equation fit this curve ?
| PowerPoint PPT presentation | free to download
Polynomial and Rational Functions
| PowerPoint PPT presentation | free to download
Adding and Subtracting Polynomials ALGEBRA 1 LESSON 9-1 (For help, go to Lesson 1-7.) Simplify each expression. 1. 6t + 13t 2. 5g + 34g 3. 7k 15k 4. 2b 6 + 9b
| PowerPoint PPT presentation | free to download
You are designing a marble basin that will hold a fountain for a city park. The basin's sides and bottom should be 1 foot thick. ...
| PowerPoint PPT presentation | free to view